Opinion: Influence of the mean free path of air on atmospheric particle growth
Recent studies by Tsalikis et al. (2023, 2024) predicted that the mean free path of air (λair) could be significantly smaller than widely used values by a factor of ∼ 2. Given the fundamental importance of λair, the question of whether an overestimation of λair would have profound influence on a number of aerosol processes must be answered. Here we assume that the newly proposed value of λair is accurate and examine its influences on our understanding of atmospheric aerosols. We show that for collision-induced aerosol dynamics such as the condensation growth of atmospheric particles, the collision rate and hence the growth rate are determined by an effective mean free path for vapor and particle collision rather than by λair. Similar to the cause of a smaller λair, the overlooked force field in pure elastic models may enhance vapor–particle collisions; however, this enhancement has been accounted for in previous studies. As a result, we find that the smaller λair does not substantially influence particle collisions; i.e., it does not challenge our previous understanding of particle growth in the lower troposphere. Other potential influences on growth involving high excess latent heat and the uncertainties in the sub-5 nm size range are also addressed.
The mean free path is a fundamental quantity in aerosol research. It is widely used to characterize the regime of particle motion in surrounding gases and is closely associated with particle dynamic processes such as deposition, diffusion, condensation, and coagulation. Recently, Tsalikis et al. (2023, 2024) investigated the mechanics and dynamics of collisions of air molecules (i.e., nitrogen and oxygen) and revisited the values of the mean free path of air (λair). Using a thoroughly validated atomistic molecular dynamics model, they proposed that the air molecules collide more frequently with each other compared to previous understandings. The force field, previously neglected in pure elastic models, was found to be the governing reason for the more frequent collisions. As a result, λair was predicted to be significantly smaller than the widely used values. For example, the newly proposed value of λair at 300 K and 1 atm is 38.5 nm, while the widely used value is 67.3 nm. However, the effects of this change in the value of λair remain unclear. Here we assume that the newly proposed value of λair is accurate and examine the influence of λair on the dynamic processes of atmospheric aerosols.
We mainly focus on the collision rate between vapor molecules and aerosol particles and, subsequently, the growth rate of particles. This is motivated by the importance of growth to the atmospheric and to the climatic influences of airborne particles (Kulmala et al., 2022). If particles grew faster than previously expected, they could form more cloud condensation nuclei and provide more surface for atmospheric physicochemical processes. However, we find that despite the significant change in the value of λair, it has negligible influence on particle growth and relevant processes. That is, the framework of present-day aerosol dynamic theories, especially in typical atmospheric conditions, is not challenged by the uncertainties in the value of λair. We also note that the growth of small nanoparticles at the kinetic limit (e.g., < 3 nm) may be affected by the uncertainties associated with the force field of air molecules. The reasons are given in detail below.
The mean free path of air is the average distance an air molecule travels between its consecutive collisions with other air molecules. The relative size of a particle compared to λair determines the behavior of the air molecules surrounding it, which can be characterized by the Knudsen number (Kn),
where dp is the particle diameter, and the subscript air emphasizes that Eq. (1) is for air molecules. The movement of particles is usually classified into three dynamic regimes according to the value of Knair, i.e., the kinetic regime (or free molecular regime) for Knair ≫ 1, the continuum regime for Knair ≪ 1, and the transition regime between the kinetic and continuum regimes for Knair ∼ 1.
However, the use of the mean free path and its corresponding Knudsen number varies with the specific transfer process from vapors to particles. Fuchs and Sutugin (1971) proposed that the mean effective free path should be used, and its formula differs for mass and heat transfer processes. For the collision between particles and condensable vapors, the mean effective free path characterizes the distance the vapor molecule travels before its velocity becomes independent of the initial velocity. Here we use a modified Fuchs–Sutugin expression for condensation reported in Lehtinen and Kulmala (2003), which has an improved accuracy for particles down to molecular sizes. The Knudsen number and the mean free path are correspondingly defined as
where D is the diffusion coefficient, c is thermal velocity, and the subscripts v and p indicate vapor and particle, respectively. Different from Eq. (1), the Kn in Eq. (3) is determined by the mean effective free path for vapor and particle collision, λ, instead of λair.
For the convenience of illustration, we first discuss the collision between vapors and small nanoparticles at the kinetic limit (Kn → ∞). The collision coefficient can be expressed as
where K is the collision coefficient and the subscript K indicates the kinetic limit, α is the mass accommodation coefficient and is taken to be 1 in this study, m is mass, E characterizes the enhancement of intermolecular forces on the collision coefficient compared to pure elastic collisions, A is the Hamaker constant, k is the Boltzmann constant, and T is temperature. Here the relative thermal velocity between the colliding vapor and particle is explicitly expressed by their masses.
Equation (4) shows that the collision coefficient at the kinetic limit is governed by the collision cross-section and the relative thermal speed. While the relative thermal velocity is determined by the masses of vapor and particles, there may be uncertainties in the collision cross-section calculated using the vapor and particle diameters. Previous studies have shown that electrical mobility diameter inferred from measured electrical mobility using the Stokes–Millikan equation deviates from the mass diameter (Tammet, 1995; Ehn et al., 2010; Larriba et al., 2011). Furthermore, as characterized by E in Eq. (4), the attractive component of the force field extends the time that colliding vapor and particles stay close to each other. This is equivalent to increasing the collision cross-section for air molecules compared to pure elastic collisions. For instance, experimental evidence shows that van der Waals forces enhance the growth rate of newly formed particles by a factor of ∼ 2 compared to growth by pure elastic collisions (Stolzenburg et al., 2020). This enhancement is also supported by molecular dynamic simulations for the collision between two sulfuric acid molecules (Halonen et al., 2019). Tsalikis et al. (2023, 2024) found similar influences of the force field on the collision cross-section of air molecules, which is the governing reason for the smaller λair predicted by molecular dynamic models compared to pure elastic models. We also note that the values of λair and λ are not used in computing the collision coefficient using Eq. (4); however, the influence of the force field of air molecules on the collision between vapors and particles remains to be further investigated.
For collisions during the continuum and transition regimes, the collision coefficient between particles and vapors can be expressed as
where βm is the Fuchs–Sutugin semi-empirical factor. At the continuum limit (Kn → 0), βm approaches 1, and Eq. (5) can be simplified as
where the subscript C indicates the continuum limit. At the kinetic limit (Kn → ∞), it can be verified that Eq. (5) can be simplified to Eq. (4); i.e., the value of K computed using Eq. (5) converges to the value of KK in Eq. (4) at the kinetic limit.
Finally, the growth rate of monodisperse particles due to vapor condensation can be obtained by multiplying the collision rate and the increment of particle size per collision, yielding
where Nv is the concentration of vapor molecules, is the equilibrium vapor concentration after considering the Kelvin effect and the effect of Raoult's law, and Δdp is the increment in particle diameter after adding a vapor molecule. For spherical particles, Δdp can be expressed as . Equations (2)–(8) can also be applied to coagulation processes by replacing the condensation vapors with particles, yet here we focus on condensation processes for the convenience of understanding.
For the convenience of understanding, we show the particle growth rate driven by the condensation of 107 cm−3 gaseous sulfuric acid in Fig. 1. The sulfuric acid is assumed to be nonvolatile, and the Hamaker constant is taken to be 4.6 × 10−20 J. According to Tsalikis et al. (2024), a molecular dynamic simulation reproduced the values for the density, diffusion coefficient, and dynamic viscosity of air in experimental measurements or theoretical expressions well, and the air velocity distribution was identical to the classical expression. Equation 4 shows that the collision coefficient at the kinetic limit is determined by the sizes and thermal velocities of vapors and particles; i.e., it is not affected by λair. Similarly, Eq. (7) shows that with the given diffusion coefficients and thermal velocities, λair does not influence the collision coefficient. Indeed, the diffusion coefficient of particles is calculated using λair; however, we will show in the discussion below that updating the value of λair does not practically affect particle diffusion. For the transition regime (0.1 < Kn < 10), the formulas for the kinetic and continuum limits tend to overestimate the collision coefficient, and the Fuchs–Sutugin factor βm needs to be used. However, λair is not used to calculate the value of βm for vapors and particles with given diffusion coefficients and thermal velocities (Eqs. 2, 3, and 5). As a result, updating the value of λair changes neither the particle growth rate nor the size range corresponding to the kinetic, transition, and continuum regimes for vapor condensation (Fig. 1).
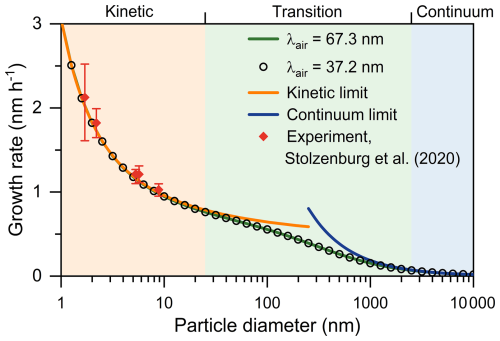
Figure 1Particle growth rate by the condensation of sulfuric acid. The sulfuric acid concentration is 107 cm−3. Lines and open markers are the theoretically predicted results using Eqs. (4)–(8). The shaded areas indicate the dynamic regimes for collision, i.e., the kinetic regime (Kn ≥ 10), the transition regime (0.1 < Kn < 10), and the continuum regime (Kn ≤ 0.1). Closed markers indicate the experimentally determined growth rate from chamber experiments reported by Stolzenburg et al. (2020).
The governing reason for the smaller λair predicted by molecular dynamic models compared to pure elastic models is that the attractive component of the force field extends the time that colliding molecules stay close to each other. This is equivalent to increasing the collision cross-section for air molecules compared to pure elastic collisions. As shown in Fig. 2, the measured particle growth rate of sub-10 nm particles exceeds the prediction by a pure elastic model (A = 0 and hence E = 1 in Eq. 5), in which the condensing vapor (sulfuric acid) is assumed to be nonvolatile, and the growth rate is hence limited by the collision rate. This indicates a non-negligible collision enhancement of the force field between vapors and particles. With such a force field, the effective collision cross-section is expected to be larger than that in the pure elastic model, and the mean effective free path (λ) is correspondingly smaller than that predicted in Eq. (3). While noting that the influence of the force field on λ is expected to be size-dependent, we arbitrarily reduce the value of λ by a constant factor of 2 and show relatively good consistency between the measured and predicted sub-10 nm growth rate.
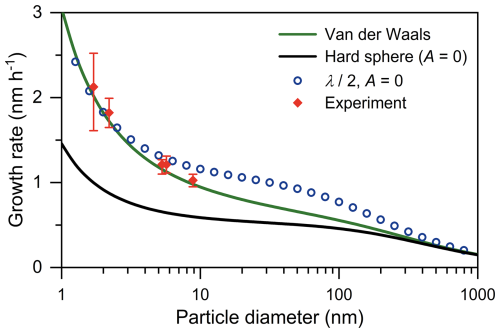
Figure 2Influence of the force field on the particle growth rate. The growth rate is calculated for the condensation of nonvolatile sulfuric acid with a concentration of 107 cm−3. The green line (van der Waals) indicates the results calculated using Eq. (5) with a Hamaker constant (A) of 4.6 × 10−20 J. The black line (hard sphere) is calculated using a pure elastic model in which particles and vapors are taken as hard spheres, i.e., by setting the value of A in Eq. (5) to 0. Open markers indicate the growth rates with λ values hypothetically divided by a factor of 2. Closed markers are from Stolzenburg et al. (2020).
However, previous studies have used a semi-empirical correction factor E (see Eqs. 4, 5, and 7) to account for collision enhancement due to the force field between vapors and particles. With a Hamaker constant of 4.6 × 10−20 J, the growth rate predicted using Eq. (4) can reproduce the measured data without adjusting the value of λ (Fig. 2). That is, the influence of the force field on vapor condensation has been accounted for in present-day particle growth studies, although this is not achieved by explicitly updating the value of λ. Previous studies (e.g., Stolzenburg et al., 2020) have also discussed the uncertainty in E, which is associated with the uncertainty in λ for growth rate calculation. Regardless of which method is implemented for this enhancement, it is important to avoid double counting: if one uses the van der Waals correction factor E for the force field, one should not adjust λ and vice versa.
The diffusion coefficient of particles is a function of λair. The diffusion coefficient Dp can be expressed as
where Cs is the Cunningham slip correction factor; μ is the viscosity of air; and a, b, and c are fitting parameters for the Knudsen–Weber formula for Cs.
Equations (9)–(10) indicate that the value of λair influences particle diffusion by influencing Cs. However, these influences do not apply to the update of λair proposed by Tsalikis et al. (2023, 2024). This is because the values of the fitting parameters in Eq. (10) were obtained as the best fit to experimental results with a predetermined value of λair. Updating the value of λair corresponds to an update in the values of the fitting parameters rather than the values of Cs. For instance, the values of a, b, and c reported in Allen and Raabe (1985) for spherical solid particles for λair = 67.3 nm at sea level and at 23 °C are 1.142, 0.558, and 0.999, respectively. If λair is updated to 38.5 nm at the same temperature and pressure, a, b, and c should be correspondingly updated to 1.996, 0.975, and 1.746, respectively, to be consistent with experimental results from the Millikan oil-drop experiments. For the same reason, updating the value of λair by accounting for the force field for collisions is not expected to directly affect other processes relevant to the drag force of air molecules on particles at atmospheric conditions, e.g., coagulation, agglomeration, and electrical motion, although indirect influences may exist. It is also worth clarifying that when applying Eq. (5) to the kinetic limit, the diffusion coefficients in Eq. (5) cancel out those in βm (see also Eq. 4). Consequently, the uncertainty in Eq. (9) for small nanoparticles (e.g., < 3 nm) does not propagate into the value of K.
For the rapid condensation of vapor molecules with high latent heat, the heat transfer from growing aerosol particles needs to be considered (e.g., Yang et al., 2019). In these situations, the temperature at the aerosol surface can be significantly higher than the ambient air temperature. One typical example in the atmosphere is cloud droplet formation, during which supersaturated water vapor condenses on cloud condensation nuclei (ca. 100 nm) within a few minutes to form cloud droplets (ca. 10 000 nm) (e.g., Kulmala et al., 1993). Different from the Kn for vapor condensation in Eq. (3), the Knudsen number for heat transfer should be Knair, which is defined based on λair. However, since the heat and mass transfer for cloud droplet formation occurs mainly in the continuum regime, the droplet growth rate has a negligible dependence on λair.
In summary, we find that the smaller λair predicted by atomistic molecular dynamics, compared to the widely used values predicted by pure elastic collision models, does not substantially influence particle growth by condensation and coagulation. This is because the collision of particles is determined by the mean effective free path of condensable vapors rather than by λair, and the formula for the slip correction factor is fitted to experimental results with a predetermined value of λair. The influences of the force field of air molecules on the collision between vapors and particles may need further investigation. For rapid growth processes involving high excess latent heat, a smaller λair affects growth by increasing heat transfer flux. However, this is not the case for atmospheric nanoparticle growth in the lower troposphere, and it has only a minor influence on cloud droplet formation.



