Growth of atmospheric freshly nucleated particles: a semi-empirical molecular dynamics study

When simulating new particle formation rates, collisions in the system are approximated as hard spheres without long-range interactions. This simplification may lead to an underestimation of the actual formation rate. In this study, we employ semi-empirical molecular dynamics (SEMD) at the GFN1-xTB level of theory to probe the sticking process of the monomers sulfuric acid (SA), methanesulfonic acid (MSA), nitric acid (NA), formic acid (FA), ammonia (AM), methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA) onto freshly nucleated particles (FNPs). The FNPs considered are (SA)₁₀(AM)₁₀, (SA)₁₀(MA)₁₀, (SA)₁₀(DMA)₁₀, and (SA)₁₀(TMA)₁₀.

In general, we find that the hard-sphere kinetic approximation, which neglects long-range interactions, significantly underestimates the number of collisions leading to sticking. By calculating the sticking coefficient from SEMD simulations, we obtain enhancement factors of 2.3 and 1.5 for the SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀ collisions, respectively. A comparison with OPLS (optimized potentials for liquid simulations) all-atom force field simulations shows similar enhancement factors of 2.4 and 1.6 for the SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀ collisions, respectively.

Compared to the force field simulations, SEMD exhibits a more isotropic sticking behavior, with the probability remaining near unity for small offsets before rapidly dropping to 0 % beyond a certain offset. In contrast, the force field simulations show a more gradual decline in sticking probability due to certain orientations still leading to sticking. The largest discrepancy between the two methods occurs at lower collision velocities – below 200 m s⁻¹ for SA and below 400 m s⁻¹ for AM – where force field simulations, even for head-on collisions, predict low or zero sticking probability. This has previously been attributed to periodic repulsions between the rotating collision partners caused by fluctuations in their charge distributions. In contrast, SEMD simulations do not exhibit this behavior. Since these low velocities are not significantly populated in our simulations, both methods yield similar enhancement factors. However, for systems with larger effective masses, where such velocities are more prevalent, we would expect the two methods to diverge.

1 Introduction

According to the Sixth Assessment Report of the IPCC, aerosols are responsible for the largest uncertainty in current global climate models, due to their ill-defined effects on the climate (Lee et al., 2023). Aerosols affect the climate by direct contact with sunlight through absorption or reflection or by acting as nucleation cores, termed cloud condensation nuclei (CCN), for water uptake and further growth into clouds (Boucher and Lohmann, 1995). Of these two factors, the uncertainty associated with the formation of CCN has the greatest impact on modeling radiative forcing (Canadell et al., 2021), and this uncertainty is mainly due to a lack of understanding of the initial formation steps leading to particles of 1.7–3.0 nm in diameter. For instance, changing the growth mechanism of 1.7–3.0 nm particles from being solely sulfuric-acid-based to including extremely low-volatility organic compounds can lead to a factor-of-2 difference in the predicted CCN number concentration (Tröstl et al., 2016). Hence, understanding the growth behavior of freshly nucleated particles, around 1.7 nm in diameter, is paramount for reducing this uncertainty.

Modeling studies show that around 30 %–60 % of CCN, over land, are formed through new particle formation (NPF), a process where atmospheric gas-phase precursors undergo gas-to-particle conversion (Boucher and Lohmann, 1995; Merikanto et al., 2009; Zhao et al., 2024). This leads to a burst of 1–2 nm freshly nucleated particles (Kulmala et al., 2013). The NPF process can, to a large extent, be explained by clustering of sulfuric acid (SA) coupled with bases of high abundances such as ammonia (AM) (Kulmala et al., 2013; Kirkby et al., 2011; Schobesberger et al., 2013; Weber et al., 1996; Elm, 2021a; Dunne et al., 2016) or high basicity such as the alkylamines methylamine (MA), dimethylamine (DMA) (Elm et al., 2020; Engsvang et al., 2023b; Kurtén et al., 2008; Loukonen et al., 2010; Nadykto et al., 2011, 2015, 2014; Jen et al., 2014; Glasoe et al., 2015; Almeida et al., 2013; Elm, 2021a), and trimethylamine (TMA) (Elm, 2021a; Kurtén et al., 2008; Nadykto et al., 2011; Jen et al., 2014; Nadykto et al., 2015; Glasoe et al., 2015). Cluster formation has also been shown to be enhanced by other acids such as nitric acid (NA) (Wang et al., 2020; Liu et al., 2021, 2018; Kumar et al., 2018; Ling et al., 2017; Wang et al., 2022; Nguyen et al., 1997; Longsworth et al., 2023; Knattrup et al., 2023; Knattrup and Elm, 2022; Bready et al., 2022; Qiao et al., 2024), formic acid (FA) (Bready et al., 2022; Knattrup et al., 2023; Ayoubi et al., 2023; Zhang et al., 2022, 2018; Harold et al., 2022; Nadykto and Yu, 2007), or methanesulfonic acid (MSA) (Elm, 2021b; Dawson et al., 2012; Chen et al., 2015, 2016; Perraud et al., 2020; Arquero et al., 2017b, a; Chen and Finlayson-Pitts, 2017; Elm, 2022).

NPF rates can be modeled using cluster distribution dynamics simulations, where so-called birth–death equations are solved for the relevant formation pathways:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{c}_i}{\mathrm{d}t}}& =\sum _{i=\mathrm{1}}^{\lfloor i/\mathrm{2}\rfloor }{s}_{j,(i-j)}{c}_j{c}_{(i-j)}+\sum _j{\mathit{\gamma }}_{(i+j)\to i}{c}_{i+j}\\ & -\sum _j{s}_{i,j}{c}_i{c}_j-\sum _j^{\lfloor i/\mathrm{2}\rfloor }{\mathit{\gamma }}_{i\to j}{c}_i,\end{array}\end{array}$$

where c_i is the concentration of cluster i, t the time, γ_i→j the evaporation of i to form j, and s_i,j the sticking coefficient for sticking collisions between i and j. The sticking coefficient s_i,j is related to the collision coefficient β_i,j through an accommodation factor α_i,j, which measures the percentage of collisions that result in a stable cluster:

$$\begin{array}{}\text{(2)}& s_{i,j}={\mathit{\alpha }}_{i,j}{\mathit{\beta }}_{i,j}.\end{array}$$

The Atmospheric Cluster Dynamics Code (ACDC) constructs the equations and invokes an ordinary differential equation (ODE) solver routine to solve the birth–death equations numerically for a given set of cluster sizes (McGrath et al., 2012). ACDC determines evaporation coefficients based on the binding free energies of the clusters, using detailed mass balance under the assumption that the evaporation rate does not change significantly from equilibrium (Ortega et al., 2012). Binding free energies are typically calculated using quantum chemistry methods, performed by searching for the cluster configuration with the lowest Gibbs free energy. In recent years, significant research efforts have focused on improving the accuracy of binding free energy calculations for clusters (Elm et al., 2020, 2023; Engsvang et al., 2023b).

Sticking coefficients, on the other hand, are often approximated as collision coefficients calculated through kinetic gas theory; i.e., ${\mathit{\alpha }}_{i,j}=\mathrm{1}$. In this framework, the collision partners are represented by hard spheres of defined radii, without any long-range interactions between them, meaning that a clustering event only occurs if the hard spheres overlap. By default, ACDC employs this approach to calculate sticking coefficients. In reality, atmospheric molecules and clusters interact through long-range interactions, which can significantly enhance the collision coefficient. Furthermore, it is not clear if the unit accommodation factor is a reasonable approximation for all clusters of interest in NPF.

Experimentally, Stolzenburg et al. (2020) showed that the growth rates of uncharged SA particles from 1.8 to 10 nm exceed the hard-sphere kinetic limit for the condensation of SA. Similarly, Stolzenburg et al. (2018) studied growth with organics in the 2–30 nm range and found that organic condensation drives particle growth. However, measurements of particles at and below 1.7 nm in diameters are lacking.

Recently, several studies have used molecular dynamics (MD) simulations to model sticking coefficients of atmospherically relevant systems. MD simulations track the system's dynamic evolution, directly accounting for dynamical effects such as the explicit temperature, i.e., the thermal motion. This is unlike the statistical thermodynamic treatment employed in quantum chemistry, where results are “extrapolated” to the given temperature from the 0 K structure.

The choice of the potential energy surface (PES) on which the nuclei move determines the character of an MD simulation. In classical MD, the PES is parametrized based on classical mechanics terms of intra- and intermolecular interactions. These functions are relatively simple, allowing for simulations of large molecular systems, but bonds are usually based on a harmonic potential and therefore cannot model bond breaking. By contrast, in Born–Oppenheimer MD (BOMD), the forces (the derivatives of the PES) are obtained directly from electronic-structure calculations by solving the time-independent Schrödinger equation. In principle, BOMD can employ any level of theory to compute energies and forces, but this rapidly becomes prohibitively expensive for large systems. Semi-empirical methods strike a practical compromise by replacing the most computationally intensive components with parametrized, empirical expressions. While these methods introduce approximations, they remain rooted in an electronic-structure framework and thus retain the ability to simulate bond breaking and formation.

Yang et al. (2018) used a force field molecular dynamics setup to study collisions of Au and Mg atoms and clusters and quantify the collision coefficient. Halonen et al. (2019) used a similar setup to study the collision between two SA molecules, finding a collision coefficient 2.2 times larger than that predicted by kinetic gas theory. Yang et al. (2023) investigated collisions of SA and DMA molecules with bisulfate–dimethylammonium clusters containing up to 16 dimers using similar force field methods. They observed that the enhancement over kinetic gas theory decreases with increasing cluster size. Other force field MD studies have explored the formation of small atmospheric clusters of SA with W or bases (Anderson et al., 2008; Loukonen et al., 2014b) or with ions (Neefjes et al., 2022; Halonen et al., 2023).

However, classical force field methods cannot model bond breaking and, therefore, cannot account for chemical reactions, such as proton transfers, which are critical for stabilizing atmospheric acid–base clusters. When acid–base clusters are used as collision partners, as in Yang et al. (2023), the fixed bonds of the monomers fail to accurately represent the interactions within the cluster. Additionally, chemical reactions, such as proton transfers, cannot occur after collisions, meaning the stability and sticking efficiency of the cluster after a collision cannot be accurately assessed.

Loukonen et al. (2014a) used DFT-based MD simulations to investigate collisions of the SA–DMA and SA–DMA–W systems, finding a sticking coefficient of unity due to proton transfer reactions. However, their study was limited to head-on collisions between molecules and dimers, as DFT-based MD simulations are computationally expensive.

Cluster distribution dynamics simulations have generally been limited to relatively small clusters (e.g., 8–10 molecules) due to the increasing computational cost of binding free energy calculations for increasing cluster sizes. Recently, however, much larger atmospherically relevant systems, referred to as freshly nucleated particles (FNPs), have been studied. Engsvang and Elm (2022) and Engsvang et al. (2023a) studied (SA)_n(AM)_n clusters, with n up to 30, while Wu et al. (2023, 2024) studied (SA)_n(base)_n clusters, with n up to 15 and the bases AM, MA, DMA, or TMA. Wu et al. (2024) determined the cluster-to-particle transition point, where clusters begin to exhibit bulk particle-like properties, as occurring at cluster sizes of 8–10 acid–base pairs. These (SA)₁₀(base)₁₀ systems, with geometrical diameters reaching up to 1.8 nm, serve as ideal test systems for investigating the growth of FNPs by collisions with monomers.

In this work, we study the collisions of the FNPs (SA)₁₀(AM)₁₀, (SA)₁₀(MA)₁₀, (SA)₁₀(DMA)₁₀, and (SA)₁₀(TMA)₁₀ with the atmospheric precursor vapors SA, MSA, NA, FA, AM, MA, DMA, and TMA in the free molecular regime. The collisions were studied explicitly using Born–Oppenheimer MD at the semi-empirical GFN1-xTB level of theory (Grimme et al., 2017). The GFN1-xTB method extends beyond traditional force field approaches by enabling the modeling of chemical reactions, such as proton transfers, and accounting for the dynamical charge distribution while maintaining significantly greater computational efficiency than DFT-based MD.

By comparing sticking coefficients derived from these simulations with those predicted by kinetic gas theory and force field MD simulations, we aim to assess the impact of long-range interactions and quantum mechanical effects in modeling the growth of FNPs.

2 Methodology

2.1 Computational details

All MD simulations were carried out using the Atomic Simulation Environment (ASE) (Larsen et al., 2017). At each time step, the forces on the nuclei were calculated using the semi-empirical GFN1-xTB method (Grimme et al., 2017) using the xtb-python calculator (Grimme-Lab, 2022). Between time steps, the nuclei are propagated classically. A time step of 1 fs was used for all simulations, as it was found to be sufficient to resolve the hydrogen stretch vibration. Prior to the collision trajectory simulations, each monomer and cluster were separately equilibrated to ensure thermal equilibrium.

2.2 Equilibration procedure

Atmospheric molecules and clusters are assumed to be thermally equilibrated. To ensure the studied molecules and clusters are at thermal equilibrium before the collision simulation, we adopted the approach outlined by Halonen et al. (2023).

We equilibrated each molecule or cluster in a separate NVT (number of particles, volume, temperature) ensemble simulation, using the Langevin thermostat with a target temperature of 300 K and a time constant of 100 fs. Initially, atomic velocities were randomly assigned based on the Maxwell–Boltzmann relative velocity distributions at 300 K. The equilibration simulations were run for 10 ns for molecules and 1 ns for clusters. Thermodynamic properties were saved every 500th time step to minimize correlations between consecutive output frames. We used equipartition as the measure for thermal equilibrium, i.e., when the cumulative average of the translational, rotational, and vibrational temperature components aligns with the target. The progression of equilibration was tracked by monitoring the cumulative averages of these temperature components over time. The total instantaneous temperature T_tot at any given time step is calculated from the kinetic energy E_kin as

$$\begin{array}{}\text{(3)}& T_{\mathrm{tot}}={\displaystyle \frac{\mathrm{2}{E}_{\mathrm{kin}}}{\mathrm{3}{k}_{\mathrm{B}}N}},\end{array}$$

where N is the number of atoms and k_B the Boltzmann constant. The corresponding translational (T_tr), rotational (T_rot), and vibrational (T_vib) temperature partitions are given as

$$\begin{array}{}\text{(4)}& {\displaystyle }{T}_{\mathrm{tr}}=N\left(T_{\mathrm{tot}}-T_{\mathrm{com}}\right),\text{(5)}& {\displaystyle }{T}_{\mathrm{rot}}=N\left(T_{\mathrm{com}}-T_{\mathrm{rotate}}\right),\text{(6)}& {\displaystyle }{T}_{\mathrm{vib}}={\displaystyle \frac{N}{N-\mathrm{2}}}{T}_{\mathrm{rotate}},\end{array}$$

where T_com is the temperature after subtracting the center-of-mass (COM) motion and T_rotate the temperature after subtracting both the COM and rotational motions.

2.3 Collision simulations

The collision simulations were carried out using the velocity Verlet algorithm, approximating the atmosphere as a free molecular regime. The simulations were initialized by placing the collision partners at a COM distance of r=20 Å from each other, offset by b and with the initial relative velocity v as illustrated in Fig. 1. The motivation for the placement distance is as follows: to determine a reasonable initial distance between the collision partners, where interactions have negligible effect on the collisions, we calculated the potential of mean force between the (SA)₁₀(AM)₁₀ cluster and SA monomer along the center-of-mass distance through umbrella sampling (Torrie and Valleau, 1977) using the OPLS all-atom force field (Jorgensen et al., 1996) (see Sect. S1 in the Supplement). The potential of mean force approaches zero at around 15 Å. While this provides a good indication of the interaction strength, the GFN1-xTB method may predict slightly stronger interactions. We therefore set the initial distance to 20 Å as the overall interaction force applied over time at and beyond this point should have a negligible effect on the collision probability. The initial relative velocity was chosen based on the most probable velocity given by the Maxwell–Boltzmann relative velocity distribution:

$$\begin{array}{}\text{(7)}& v=\sqrt{{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{B}}T}{\mathit{\mu }}}},\mathit{\mu }={\displaystyle \frac{m_{\mathrm{a}}{m}_{\mathrm{b}}}{m_{\mathrm{a}}+m_{\mathrm{b}}}},\end{array}$$

where μ is the reduced mass of the combined system, m_a the mass of the FNP and m_b the mass of the monomer, and T the temperature. It is important to establish a reasonable criterion for when a sticking collision has occurred. Since we are interested in the growth of clusters, we define the criterion based on whether the collision partners remain attached at the end of the collision simulation. The collision simulation and detection algorithm work as follows:

• The simulation is run as long as the gradient of the COM distance is negative. Once the COM distance gradient becomes positive, we know the molecules either collided or passed each other.

• From this point, the simulation is run for another 2 ps while storing the COM distance gradients to determine if the molecules are attached. We chose 2 ps as tests indicated that most detachments happen within the first 1 ps.

  • No sticking collision is registered if all the gradient values are above zero because they either bounced off each other or passed each other without interacting.

  • No sticking collision is registered if some gradients are below zero but the final COM distance is 20 % above the sum of hard-sphere radii of the collision partners. This means they interacted but eventually split apart.

  • Otherwise a sticking collision is registered.

We acknowledge that this sticking collision criterion is somewhat arbitrary, as the collision partners will eventually detach given enough simulation time. However, these criteria can identify attachments that remain stable for a certain period (i.e., 2 ps) after collision. While the quantitative results may vary with different criteria, we expect these variations to be small and systematic, and, therefore, they do not affect the qualitative conclusions of this work.

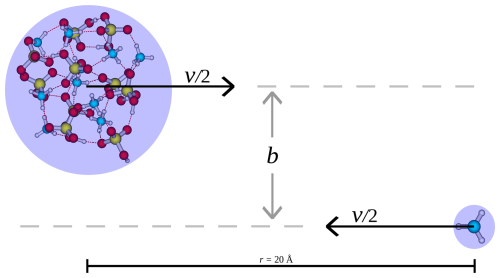
Figure 1 Illustration of the setup for the collision simulation. v is the initial relative velocity and b the perpendicular offset between the initial trajectories of the collision partners.

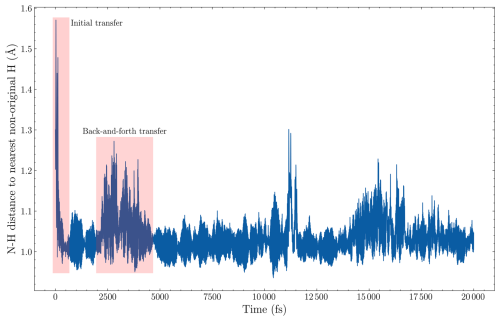
Figure 2 The distance from the nitrogen in the ammonia collision partner to the nearest hydrogen that does not originally come from the incoming ammonia monomer. The data are from one of the 300 m s⁻¹ collision simulations of AM and (SA)₁₀(AM)₁₀ from the point where a collision is detected.

To test this, we simulated a new head-on collision of the AM monomer with (SA)₁₀(AM)₁₀ at velocities of 200 and 300 m s⁻¹, tracking the collision partners 20 ps after the COM gradient change. We chose AM as we expect this to be the weakest bonding monomer. The sticking probability changed from 97 % to 98 % at 200 m s⁻¹ and from 96 % to 95 % at 300 m s⁻¹. The minimal change suggests we are capturing all the rebounding events within the 2 ps window. Interestingly, if the monomer is aligned with a hydrogen on a sulfuric acid for the initial collision, the monomer exhibits rapid hydrogen-transfer reactions within the 2 ps simulation. This can be seen from the rapid initial drop in Fig. 2, which shows the distance to the nearest hydrogen atom not originally attached to the monomer as a function of simulation time after the collision criterion has been fulfilled. Likewise, we also observe rapid back-and-forth hydrogen transfers later in the simulation when the nearest hydrogen becomes aligned with an oxygen from sulfuric acid. This behavior is exhibited as large oscillating values in the nearest-distance plot (see 2000–4500 fs in Fig. 2). Here, we define a hydrogen transfer as occurring when the distance between nitrogen and a new hydrogen drops below 1.1 Å. Accordingly, we find that the transfer occurs, for 63 % (21 % with the first 2 ps) and 58 % (11 % within the first 2 ps) of the 100 simulations, for the 300 and 200 m s⁻¹ simulations, respectively. The fast hydrogen transfer allows the monomer to be more easily incorporated into the cluster. Nevertheless, the redistribution of excess energy still plays a crucial role, as a sudden excess of translational energy on any cluster molecule can lead to the rapid loss of hydrogen and evaporation.

2.4 The sticking coefficient

The sticking coefficient s quantifies the number of sticking collisions per second per unit concentration and sets the kinetic limit for the formation of new particles. It is typically assumed to be equal to the collision coefficient derived from kinetic gas theory:

$$\begin{array}{}\text{(8)}& {\mathit{\beta }}_{\mathrm{HS}}=\sqrt{{\displaystyle \frac{\mathrm{8}{k}_{\mathrm{B}}T}{\mathit{\pi }\mathit{\mu }}}}\mathit{\pi }{\left(R_i+R_j\right)}^{\mathrm{2}},\end{array}$$

where the two collision partners are treated as non-interacting hard spheres of radius R_i and R_j, respectively, and a collision occurs only when their radii overlap. We calculate the radius of the collision partners following the implementation in ACDC (McGrath et al., 2012). Here, the radius is given by the effective volume of a sphere whose volume corresponds to the sum of the volumes of the individual monomers:

$$\begin{array}{}\text{(9)}& R={\left({\displaystyle \frac{\mathrm{3}{\sum }_{i=\mathrm{1}}^N{V}_i}{\mathrm{4}\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{3}},\end{array}$$

where the monomer volume V_i for the N monomers in the FNP are given by their molar mass and liquid bulk density.

The sticking coefficient can also be calculated from MD simulations via the probability of sticking P(v,b) for the given offset b and velocity v via numerical integration of the following expression (Neefjes et al., 2022):

$$\begin{array}{}\text{(10)}& s_{\mathrm{MD}}=\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}vf\left(v\right)P(b,v)\mathrm{d}\left(b^{\mathrm{2}}\right)\mathrm{d}v,\end{array}$$

where f(v) is the Maxwell–Boltzmann relative velocity distribution for the given initial relative velocity.

The enhancement factor is then calculated as the ratio between the coefficients:

$$\begin{array}{}\text{(11)}& \mathit{\eta }={\displaystyle \frac{s_{\mathrm{MD}}}{{\mathit{\beta }}_{\mathrm{HS}}}}.\end{array}$$

3 Results and discussion

3.1 Equilibration

As the equilibration of the collision partners is the most time-consuming step in our simulations, it is important to find the minimal amount of time needed to reach thermal equilibrium. As an example, it takes 14 min for 1000 steps in a velocity Verlet simulation of the (SA)₁₀(AM)₁₀ cluster using one CPU at GFN1-xTB. The OPLS force field takes 0.1 s for the same setup, i.e., 3 to 4 orders of magnitude faster.

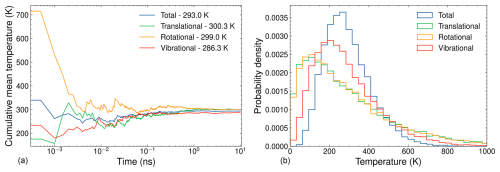
Figure 3 (a) Cumulative mean temperature as a function of simulation time and (b) temperature distribution for a 10 ns NVT simulation of ammonia. The simulation parameters include a target temperature of 300 K, a time step of 1 fs, a Langevin thermostat time constant of 100 fs, and temperature data recorded every 500 fs.

The molecule with the fewest degrees of freedom is the most challenging to equilibrate. In our case, this is the AM monomer. The left and right sides of Fig. 3 show the cumulative mean temperatures and temperature distributions, respectively, of the AM monomer over a 10 ns equilibration simulation. The temperature partitions are averages over the corresponding degrees of freedom. As such, their fluctuations generally decrease with the number of atoms in the system. Since AM has the fewest atoms among the studied systems, we would expect it to take the longest time to equilibrate. From Fig. 3 it can be seen that the cumulative mean temperatures of each temperature partition converge around the target temperature of 300 K after ∼ 1 ns. While these cumulative mean temperatures approach the target, they do not exactly reach 300 K even after 10 ns. Specifically, the translational cumulative mean temperature achieves the target of 300 K, while the total, rotational, and vibrational cumulative mean temperatures fall short by 7, 1, and 14 K, respectively. One possible explanation for this discrepancy is that the vibrational modes are treated as quantum anharmonic oscillators at the GFN1-xTB level of theory. The equipartition theorem only strictly applies to classical degrees of freedom, where the energy is a quadratic term. Classical force field MD simulations model the bonds between atoms as classical harmonic oscillators. Consequently, equilibration using this classical framework yields cumulative mean vibrational temperatures closer to the target temperature. However, even in classical simulations, some deviation from the target temperature occurs, likely due to the stochastic nature of the Langevin thermostat and numerical imprecision.

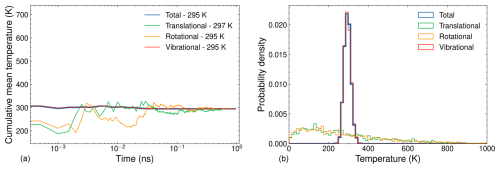
Figure 4 (a) Cumulative mean temperature as a function of simulation time and (b) temperature distribution for a 1 ns NVT simulation of (SA)₁₀(TMA)₁₀. The simulation parameters include a target temperature of 300 K, a time step of 1 fs, a Langevin thermostat time constant of 100 fs, and temperature data recorded every 500 fs.

Although the cumulative mean temperatures do not fully converge to the target temperature during equilibration, the deviations are minor and are not expected to significantly impact the collision dynamics. The largest FNP cluster we studied is the (SA)₁₀(TMA)₁₀ cluster, consisting of 200 atoms. This cluster represents our computational bottleneck due to its size. The left and right sides of Fig. 4 show the cumulative mean and distribution, respectively, of the temperature partitions for a 1 ns simulation of (SA)₁₀(TMA)₁₀. Given the large number of vibrational degrees of freedom, the vibrational temperature partition dominates the total temperature, and its cumulative value converges quickly toward the target temperature. In contrast, the translational and rotational temperatures, each with only 3 degrees of freedom, exhibit frequent fluctuations, and their cumulative means take considerably longer to converge. Compared to AM, the larger deviations from the target temperature in the cumulative means of the translational and rotational temperature partitions are due to the greater total kinetic energy in the FNP being distributed across the same number of degrees of freedom as in the monomer. Although the cumulative mean vibrational temperature is closer to the target than for AM, it still shows a deviation of 5 K. As with AM, we consider these small deviations acceptable, as they are unlikely to significantly affect the collision dynamics. The sharp distribution of the vibrational temperatures in Fig. 4 compared to Fig. 3 is due to averaging over a larger number of atoms for the FNP.

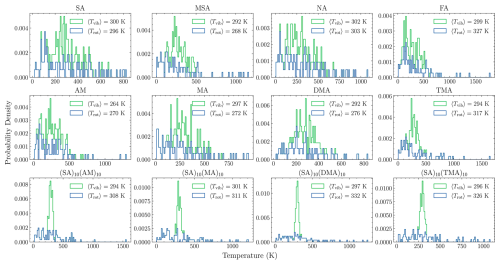
Figure 5 Distribution of rotational and vibrational temperature for the 100 output frames of the monomers and FNPs as obtained from the equilibration procedure.

From these results, we assume equilibration to have been achieved after 1 ns for the FNPs and 10 ns for the monomers. Following this equilibration, the next 100 output frames (saved every 500 fs) are used as input for the collision MD simulations. As the collision event is a non-equilibrium process for the translational degree of freedom, the center of mass is kept fixed during the equilibration and only the total, rotational, and vibrational temperatures are monitored. Figure 5 shows the distribution of the rotational and vibrational temperatures for these 100 output frames for all studied systems, as well as their average values over the 100 output frames. The average rotational and vibrational temperatures deviate by up to 32 K from the target temperature (T₀=300). This is a result of inherent temperature fluctuations within the NVT ensemble. The expected standard deviation​​​​​​​ of the temperature is given by Landau and Lifshitz (1969):

$$\begin{array}{}\text{(12)}& \text{exp-SD}=\sqrt{{\displaystyle \frac{\mathrm{2}}{N_{\mathrm{dof}}}}}{T}_{\mathrm{0}}.\end{array}$$

Overall, the standard deviations of the fluctuations align with the expected values from Eq. (12), indicating that the thermostat parameters are reasonable and well-behaved. Only the vibrational temperature of AM (SD=128 K vs. exp-SD=173 K) and the rotational temperatures of FA (297 K vs. 245 K), DMA (169 K vs. 245 K), and TMA (288 K vs. 245 K) show noticeable discrepancies, possibly due to averaging over too few output frames as the sampling error is high with fewer data. These discrepancies can be reduced by including more output frames or, alternatively, collecting structures from multiple independent equilibration runs. However, both approaches would incur a substantial increase in computational cost. Despite some deviations reaching up to 11 % from the target temperature, these variations are not expected to affect the qualitative outcomes of the collision dynamics.

3.2 Sticking probabilities

Using the equilibrated structures as the starting point, we performed 100 simulations for each offset (b) for all the studied systems. Figure 6 shows the sticking probabilities for the given monomer (title) onto the FNP given by the label for the given offset and at mode speed. The uncertainty is the Wilson score interval. The shaded gray area indicates the hard-sphere limits where the sticking probability from kinetic gas theory drops to 0 %. We see that for all systems, sticking occurs beyond the limits given by kinetic gas theory. This indicates that kinetic gas theory is likely underpredicting the collision coefficient as the clusters and monomers exhibit substantial long-range interactions that attract the collision partners toward each other.

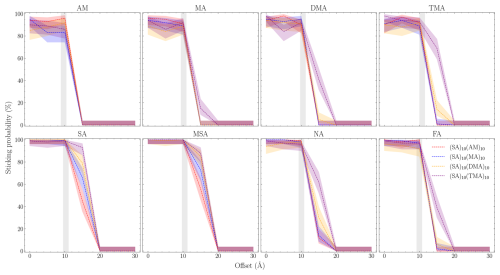
Figure 6 Number of collision simulations that satisfy the sticking criteria as a function of the offset between the collision partners. The uncertainty is the Wilson score interval (we assume binomial distribution). The gray area indicates the range between the smallest and largest sum of the hard-sphere radii of each system.

For all systems, we observe a fast drop-off beyond the hard-sphere limit. This indirectly provides a measure for the strength of the long-range interactions. The strongest long-range interaction is observed for systems with the SA and MSA monomers, where it takes roughly a 10 Å offset to reach 0 % sticking. The remaining systems reach 0 % after 4–7 Å. Generally, when the individual FNPs are distinguishable (i.e., the lines are not on top of each other), we also see a drop-off that follows TMA > DMA > MA > AM for higher sticking probability. We speculate that this trend is due to the size of the FNPs rather than the interaction strength, as the increasing number of methyl groups is expected to shield the partial charges, thereby reducing long-range interactions.

Interestingly, the sticking probability for the bases below the hard-sphere limit is not 100 % but instead hovers around 90 %. This suggests acid uptake on 1 : 1 FNPs is more favorable compared to bases, in accordance with quantum chemical calculations (Olenius et al., 2013; Elm, 2017).

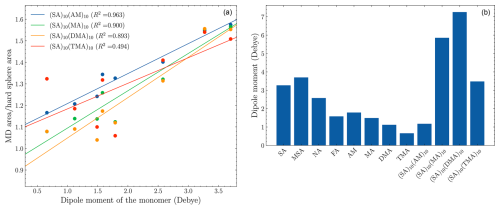
Figure 7 (a) The ratio between the area of the MD simulation in Fig. 6 and the area of probability calculated by kinetic gas theory as a function of the dipole moment of the monomer. (b) The dipole moment of the monomers calculated at the ωB97X-D/6-31++G(d,p) level of theory. The FNPs are at the B97-3c level of theory.

If the enhanced sticking probability were due to long-range interactions, we would expect the enhancement to be proportional to the dipole moment of the monomers. To probe the correlation, we calculated the integrated area of the sticking probabilities as a function of offset for the MD simulations (Fig. 6) and for kinetic gas theory (hard-sphere radii × 100 %). The ratio between the two areas should be a measure of the enhancement. The plot of the enhancement ratio versus the dipole moments of monomers and the dipole moments is shown in Fig. 7.

For the (SA)₁₀(AM)₁₀ FNP, there is almost a direct proportionality between the ratio and the dipole moments (R²=0.963). The (SA)₁₀(MA)₁₀ and (SA)₁₀(DMA)₁₀ are slightly less proportional, with R² values of 0.900 and 0.893, respectively. Lastly, the (SA)₁₀(TMA)₁₀ FNP does not exhibit a linear proportionality between the dipoles and enhancement ratio (R²=0.494). This is due to outliers (relative to the fit) of the TMA, MA, and FA monomers, which appear to exhibit an inverse trend of enhancement ratio versus dipole moments. This shows the enhancement is quite sensitive to the constituents of the FNPs and is not entirely a function of the monomer dipole moments. We speculate that the difference is due to the shielding of the partial charges in the FNPs. For instance, the (SA)₁₀(AM)₁₀ FNP has no methyl groups for shielding the partial charges, and it thus exhibits the direct proportionality, while the (SA)₁₀(TMA)₁₀ FNP has three methyl groups per base monomer and does not exhibit a strong proportionality.

Interestingly, the R² values for (SA)₁₀(MA)₁₀ and (SA)₁₀(DMA)₁₀ are remarkably similar to those of (SA)₁₀(AM)₁₀, despite the presence of additional methyl groups. We speculate that the influence of the additional methyl groups is counteracted by the accompanying increase in dipole moment, resulting in little to no change.

3.2.1 Sticking coefficient

To obtain an explicit measure of the enhancement, the sticking coefficient must be calculated. This requires simulating sticking collisions for all initial relative velocities that are significantly populated according to the Maxwell–Boltzmann relative velocity distribution. This is computationally expensive for the larger FNPs, such as (SA)₁₀(TMA)₁₀, as the low-velocity simulations would take a long time at the GFN1-xTB level. However, it is feasible for the smaller (SA)₁₀(AM)₁₀ FNP, where we simulate the SA and AM collisions for velocities of 50 and 100–1300 m s⁻¹ in increments of 100, with an offset of 0 to 30 Å in steps of 2 Å. From Fig. 8, we again observe sticking probabilities above the limit given by the sum of hard-sphere radii (green line). This is especially noticeable for the sulfuric acid collision, where the most populated velocities (100–400 m s⁻¹) have significant sticking probabilities for offsets up to 6 Å larger than the hard-sphere limit. For the SA collision, the assumption of 100 % sticking probability below the hard-sphere limit is valid for all the populated initial relative velocities. For the AM collision, this assumption does not hold, as several points below the limit have probabilities around 80 %. However, it still exhibits sticking probability beyond the hard-sphere limit, but it only extends for 2 Å at the most populated velocities (400–700 m s⁻¹). AM being less likely to form stable clusters compared to SA is consistent with quantum chemical calculations, which indicates that cluster growth tends to favor acid-first formation followed by base addition (Olenius et al., 2013; Elm, 2017; Kubečka et al., 2023b).

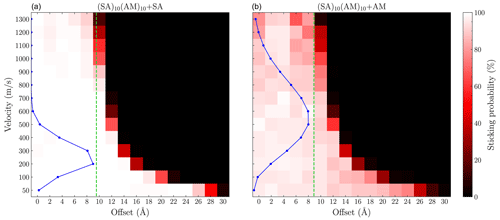
Figure 8 Grid of the sticking probability for the (a) SA + (SA)₁₀(AM)₁₀ and (b) AM + (SA)₁₀(AM)₁₀ collisions as a function of the offset and velocity. Each point was simulated 100 times using GFN1-xTB. The blue points show the Maxwell–Boltzmann distribution at the relative velocity. The green line indicates the sum of the hard-sphere radii of the system.

Following the edge along the exponentially decreasing curve, the systems exhibit a sharp drop to zero probability. This indicates that the interactions and uptake process behave isotropically. If the sticking probability were strongly orientation-dependent, we would expect a more gradual drop-off as a function of offset because a subset of the possible orientations would lead to sticking. It should be noted that this is less pronounced for the AM collision, as it shows more variation in the sticking probabilities as a function of the offset, especially for the lower velocities (50–200 m s⁻¹). However, these are mostly in the 80 %–99 % range and are therefore still not strongly orientation-dependent.

Integrating the attachment probability using Eq. (10), we find an enhancement factor η of 2.3 and 1.5 for the SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀ collisions, respectively. The SA enhancement factor also matches the one found by Yang et al. (2023) (roughly 2.5) for the SA + (SA)_n(DMA)_n collision using the OPLS all-atom force field at similar sizes. It should be noted that these enhancement factors are quite sensitive to the grid sizes simulated and the chosen numerical integration method. Therefore, rounding to the nearest half point is reasonable given the uncertainty. For both systems, we underestimate the collision coefficient when using the hard-sphere model. The enhancement scales with the interaction strength, as the stronger interacting SA molecule has an enhancement of roughly 2, while the weaker interacting AM molecules only exhibit an enhancement of 1.5. While not all AM collisions below the hard-sphere limit have a sticking probability of 100 %, the increased probability from the ranged interactions still results in an enhancement factor above 1.

If all collisions in the ACDC simulation include an enhancement factor of 2, the simulated new particle formation rate doubles. This indicates that the standard ACDC settings may underestimate the actual new particle formation rate.

3.2.2 Comparison with force field methods

To compare the sticking probabilities from the semi-empirical method with those from force field calculations, we performed simulations for the same system using the methodology of Yang et al. (2023), employing the OPLS all-atom force field (see Fig. 9).

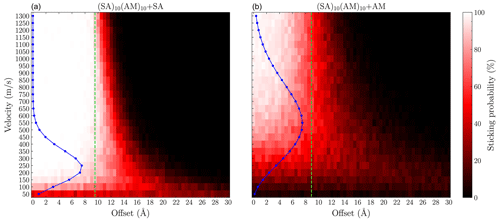
Figure 9 Grid of the sticking probability for the (a) SA + (SA)₁₀(AM)₁₀ and (b) AM + (SA)₁₀(AM)₁₀ collisions as a function of the offset and velocity. Each point was simulated 200 times using the OPLS force field. The blue points show the Maxwell–Boltzmann distribution at the relative velocity. The green line indicates the sum of the hard-sphere radii of the system.​​​​​​​

We find the force field enhancement factors η to be 2.4 and 1.6 for the SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀ collisions, respectively. While the enhancement factors are similar to the GFN1-xTB simulations, the sticking behavior is quite different. The force field method exhibits a more gradual decrease in the probability as a function of offset, suggesting a more anisotropic behavior compared to GFN1-xTB. For lower velocities, sub-200 m s⁻¹ for SA and sub-400 m s⁻¹ for AM, we observe sticking probability at or below 50 % almost independently of the offset. This has previously been attributed to periodic repulsions between the rotating collision partners due to the orientation of their fixed charge distributions (Halonen et al., 2019). However, this behavior does not occur in the GFN1-xTB calculations. The electron distribution modeled by the semi-empirical method is able to accommodate the relative orientations between the collision partners during their flight, resulting in the isotropic behavior. This discrepancy does not lead to substantial differences in the enhancement factor, as only a small fraction of the total collision system population occupies these low relative velocities. However, we would expect the enhancement factor of the two methods to diverge for larger effective masses, where the lower velocities are more significantly populated. Likewise, we would also expect the two methodologies to differ for sticking events where reactions are extremely important. For instance, hydrogen-transfer reactions for cluster and monomer collision that would form a cluster with a 1 : 1 acid–base ratio will make the monomer stick more strongly. However, force field simulations would not capture this, as most force field methods are unable to simulate bond breaking and formation.

4 Conclusions

We investigated the sticking process of the atmospherically relevant monomers sulfuric acid (SA), methanesulfonic acid (MSA), nitric acid (NA), formic acid (FA), ammonia (AM), methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA) onto freshly nucleated particles (FNPs). The FNPs considered are (SA)₁₀(AM)₁₀, (SA)₁₀(MA)₁₀, (SA)₁₀(DMA)₁₀, and (SA)₁₀(TMA)₁₀. The simulations were performed using semi-empirical molecular dynamics (SEMD) at the GFN1-xTB level of theory, which, unlike classical force field methods, accounts for chemical reactions and the dynamic charge distribution.

Using the equipartition theorem as a measure for thermal equilibrium, we find that the collision partners require an equilibration run of 10 ns for the monomers and 1 ns for the FNPs. Equilibration was performed using the Langevin thermostat targeting 300 K, with a thermostat time constant of 100 fs and a time step of 1 fs.

Carrying out the simulations using the equilibrated collision partners, we find that the hard-sphere kinetic approximation, which neglects long-range interactions, significantly underestimates the number of collisions leading to sticking. Comparing the acids and bases, the acids show a higher probability due to the increased long-range interaction strength. Furthermore, the sticking probability for the bases below the hard-sphere limit is not 100 % but instead hovers around 90 %.

We find enhancement factors of 2.3 and 1.5 for SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀, again confirming that kinetic gas theory underestimates the sticking probability. Comparing the enhancement factors with those obtained from OPLS all-atom force field simulations, we find similar values of 2.4 and 1.6 for the SA + (SA)₁₀(AM)₁₀ and AM + (SA)₁₀(AM)₁₀ collisions, respectively. Although the enhancement factors are similar, there are two major differences: (1) at lower collision velocities – below 200 m s⁻¹ for SA and below 400 m s⁻¹ for AM – force field simulations predict low or zero sticking probability, even for head-on collisions. (2) In the semi-empirical simulations, the sticking probability remains near unity for small offsets and then drops sharply to 0 % beyond a certain offset, exhibiting an almost isotropic behavior. In contrast, the force field simulations show a more gradual decline in sticking probability, suggesting anisotropic behavior, where certain orientations still lead to sticking, while others do not.

The first point accounts for the largest difference in sticking probabilities, but since these velocities are not significantly populated in our simulations, both methods yield similar enhancement factors. However, for systems with larger effective masses, we expect the enhancement factors from force field and semi-empirical methods to diverge. Additionally, for sticking events where hydrogen-transfer reactions are important (e.g., when going from a non-diagonal cluster to a cluster with a 1 : 1 acid–base ratio), the semi-empirical method will likely predict higher sticking probabilities.

This study demonstrates the use of semi-empirical methods in simulating particle formation dynamics. These methods overcome the limitations of classical force field approaches while remaining efficient enough to enable a sufficient number of simulations for accurately calculating sticking coefficients. This represents a step toward more accurate simulations of atmospheric particle formation and growth processes.