A theory-informed, experiment-based constraint on the rate of autoxidation chemistry – an analytical approach

Autoxidation is a key process that transforms volatile organic compounds into condensable species, thereby significantly contributing to the formation and growth of airborne particles. Given the enormous complexity of this chemistry, explicit reaction mechanisms describing autoxidation of the multitude of atmospherically relevant precursors may appear out of reach.

The present work suggests an alternative solution path: based on theoretically suggested key reaction types and the recent advances in mass spectroscopy, an analytically based approach for constraining lumped autoxidation reaction schemes is presented. Here, the method is used to equip an autoxidation reaction scheme for α-pinene with rate coefficients based on the interpretation of simulated data. Results show the ability to recover the rate coefficients with a maximum error of less than 1 % for all reaction types. The process is automated and capable of determining roughly 10³ rate coefficients per second when run on a PC. Currently, the method is applicable to chemical systems in a steady state, which can be established in flow reactors. However, extending the concept to allow analysis of evolving systems is part of ongoing work.

1 Introduction

Volatile organic compounds (VOCs) have been detected in every environment around the globe (Blake and Blake, 2003). In the atmosphere, they react with radicals or sunlight to form oxidised species fuelling the formation of secondary organic aerosol (SOA; Hallquist et al., 2009). SOA is considered to substantially contribute to the ambient aerosol particle mass and number (Jimenez et al., 2009), thereby impacting air quality (Daellenbach et al., 2020) and climate (IPCC, 2023).

Descriptions of VOC oxidation typically consider the decomposition of the carbon structure, ultimately leading to the formation of CO₂ (Kroll and Seinfeld, 2008). However, in the last decade, the process of autoxidation, leading to accumulation of oxygen at the carbon-centred radicals, was found to be relevant under atmospheric conditions (Jokinen et al., 2014; Rissanen et al., 2014). Prior to this, auto-ignition (i.e. gas-phase autoxidation) was associated with combustion processes (Cox and Cole, 1985; Wang and Sarathy, 2016). This process can be described as follows: alkoxy (RO•) and peroxy (RO₂•) radicals undergo sequential intra-molecular hydrogen abstraction and addition of O₂ to form a RO₂• species (Crounse et al., 2013; Mentel et al., 2015; Vereecken and Peeters, 2010). The advancing enrichment of oxygen alters the species properties: the molecule's polarity and weight increase, leading to a decrease in the saturation vapour pressure.

The present paper introduces a novel, semi-empirical way of quantifying autoxidation reactions. Autoxidation under ambient conditions currently lacks a VOC-specific mechanistic description and consequently is not well represented, even in detailed atmospheric chemistry models, such as the Master Chemical Mechanism (MCM v.3.3.1: Jenkin et al., 2003; Saunders et al., 2003) or the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A: Aumont et al., 2005; Camredon et al., 2007). As a result, even detailed aerosol chemistry models applying the MCM additionally require a general description of autoxidation chemistry (Clusius et al., 2022; O'Meara et al., 2021; Roldin et al., 2014). Large-scale models, typically, may consider the contribution of autoxidation implicitly by applying empirical mass (or low-volatility species) yields to the oxidation of a VOC species (Bergman et al., 2022). These yields are obtained in experimental setups and represent the hitherto incomprehensible complexity of autoxidation chemistry using a single number or function: the aerosol particle mass or yield of low-volatility species that forms upon consumption of a certain amount of VOC by a specific oxidant (e.g. Kroll et al., 2005; Kroll and Seinfeld, 2008). It is unclear whether and how such experimentally derived particle mass yields can represent process dependencies that may occur under atmospheric conditions.

Mechanistic approaches, aiming to understand the rearrangements of the specific molecular structures leading to the oxidative molecular growth, are limited by the enormous number of chemical species formed in the chemistry: the number of molecular structures present during the degradation of n-alkanes is roughly 10^nC−1 (with nC being the number of carbon atoms in the parent structure; Aumont et al., 2005). This omits the additional complexity contributed by autoxidation (Bianchi et al., 2019; Franzon et al., 2024; Rissanen et al., 2015). To explicitly predict the evolution of the chemistry, the most important reaction pathways would need to be identified and quantified. Owing to the sheer number of species, such an approach is not possible.

Clearly, any approach aiming to capture this overwhelmingly complex system requires simplifications. Such a simplification is provided by the volatility basis set (VBS; Donahue et al., 2006, 2011; Schervish and Donahue, 2020) approach that distributes the products of simplified (autoxidation) chemistry into volatility bins. The formal scale (i.e. relatively few equations) of the method allows for application in large-scale models (e.g. Shrivastava et al., 2024; Tsimpidi et al., 2010). However, due to the lumping of the chemistry, it may be difficult to relate the model parameters to actual measurable quantities. Nevertheless, the VBS approach enables consideration of autoxidation-specific aspects in atmospheric models. The method is highly valuable in that it will enable any future mechanistic model of the (autoxidation) chemistry to be reduced to a similar form. However, the required mechanistic underpinning to do so is, as yet, missing, and a promising methodology to overcome this remains to be proposed.

A recent study (Roldin et al., 2019) considers a collective behaviour of the peroxy radicals of similar atomic composition. This greatly reduces the complexity of the system whilst still allowing description of key autoxidation chemistry (autoxidation of RO• and RO₂•) and competing reactions (mainly ${\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}/\mathrm{NO}\mathrm{•}/{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}$, including adduct formation).

This approach requires inputs for mechanistic constraint. That is, it needs to be related to some observations in order to derive rate coefficients for the lumped reactions. The input data require sampling at high atomic resolution, with known (ideally uniform) instrument sensitivity and molecular specificity.

It can be assumed that the nitrate chemical ionisation mass spectrometer (${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS) is able to provide such data (Ehn et al., 2014; Jokinen et al., 2012):

• 1.

  It is considered highly sensitive to the most oxidised species (Hyttinen et al., 2018).

• 2.

  It provides information on the chemical composition of the detected species.

• 3.

  It is an online tool providing timely resolution and enabling us to capture the evolution of closed-shell species and peroxy radicals.

Authors, previously, interpreted the signal intensity of the ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS as a concentration enabling determination of rate coefficients for accretion product formation from RO₂•+RO₂• reactions (Berndt et al., 2018a, b) or determination of extremely low-volatility VOC (ELVOC) yield (Ehn et al., 2014). In the present work we, too, use the interpretation of the ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS signal as a concentration. We systematically employ the approach by Roldin et al. (2019) to set up chemical reaction schemes describing autoxidation chemistry using a recently developed tool (Pichelstorfer et al., 2024).

A new analytically based method for determining the rate coefficients for autoxidation reaction schemes is presented. We demonstrate mathematically that the new method can be used to find rate coefficients that can plausibly describe the chemical species' evolution based on simulated mass spectra. The method compares concentrations of detected species (at atomic resolution, e.g. by ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS) and their change rates (with respect to time) to isomers that exist in a proposed lumped reaction scheme (Pichelstorfer et al., 2024). Assumptions about the relative magnitudes of the isomer-forming rate coefficients and a description of the physical change parameters (e.g. dilution or wall interaction) allow calculations of reaction rate coefficients of the proposed scheme.

2 Methods

In order to relate the evolution of the CIMS signal (equivalent to the measured concentration) to rate coefficients of an autoxidation scheme, a list of reactions likely governing the chemistry must be assumed. This list includes the autoxidation reaction of alkoxy and peroxy radicals as well as competing reaction pathways leading to the formation of closed-shell (CS) and RO• species.

Generally, each peroxy radical can interact with any other peroxy radical to form either accretion products (ROOR^′: Berndt et al., 2018b), alkoxy radicals (Crounse et al., 2013), or hydroxyl (ROH) and carbonyl (RC=O) species in a complex chemical reaction (see Orlando and Tyndall, 2012; Salo et al., 2022). In the present work, the accretion product formation is considered explicitly, as the product contains information on the reactants (i.e. the atomic composition of ROOR^′) necessary for mechanistic traceability.

$$\begin{array}{}\text{(R1)}& {\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{RO}}_{\mathrm{2}}^{\prime }\mathrm{•}\to {\mathrm{ROOR}}^{\prime }\left(+{\mathrm{O}}_{\mathrm{2}}\right)\end{array}$$

However, the formation of RO•, ROH and RC=O only provides information on one reactant (since the product does not contain information on the second reaction partner R^′). Accordingly, they are described in a lumped way, as the reaction with the sum of peroxy radicals in the system (i.e. $\mathrm{\Sigma }\left[{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\right]=\left[{\mathrm{RO}}_{\mathrm{2},\mathrm{1}}\mathrm{•}\right]+\left[{\mathrm{RO}}_{\mathrm{2},\mathrm{2}}\mathrm{•}\right]+\left[{\mathrm{RO}}_{\mathrm{2},\mathrm{3}}\mathrm{•}\right]+\mathrm{\dots }+\left[{\mathrm{RO}}_{\mathrm{2},\mathrm{n}}\mathrm{•}\right]$ with n different peroxy radicals in the system).

$$\begin{array}{}\text{(R2a)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{ROH}\left(+{\mathrm{O}}_{\mathrm{2}}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\right)\text{(R2b)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{RC}=\mathrm{O}\left(+{\mathrm{O}}_{\mathrm{2}}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\right)\text{(R2c)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{RO}\left(+{\mathrm{O}}_{\mathrm{2}}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\right)\text{(R2d)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\to \text{fragmentation products}\left(+\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\right)\end{array}$$

Reactions (R2a)–(R2d) do change the reacting peroxy radical's concentration but have only a minor effect on ΣRO₂•. This approach does not conserve the number of H atoms in the system but greatly reduces the number of those reaction equations that are difficult to constrain. Details of this approach can be found elsewhere (Jenkin et al., 2003; Saunders et al., 2003).

Other reaction pathways of RO₂• include the interaction with HO₂• (Orlando and Tyndall, 2012). In the present work, we consider the following product pathways.

$$\begin{array}{}\text{(R3a)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{ROOH}\text{(R3b)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{RO}\mathrm{•}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}\mathrm{•}\text{(R3c)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}\to \text{fragmentation products}\end{array}$$

Further, the interaction of RO₂• and NO• (Orlando and Tyndall, 2012) is considered.

$$\begin{array}{}\text{(R4a)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{NO}\mathrm{•}\to {\mathrm{RONO}}_{\mathrm{2}}\text{(R4b)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{NO}\mathrm{•}\to \mathrm{RC}=\mathrm{O}+\mathrm{OH}\mathrm{•}+{\mathrm{NO}}_{\mathrm{2}}\text{(R4c)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{NO}\mathrm{•}\to \mathrm{RO}\mathrm{•}+{\mathrm{NO}}_{\mathrm{2}}\text{(R4d)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+\mathrm{NO}\mathrm{•}\to \text{fragmentation products}\end{array}$$

Reactions (R1)–(R4) mainly represent reactions which can terminate autoxidation, though there are some branches forming RO• which allow autoxidation to continue (Reactions R2c, R3b and R4c). In the present work, the intra-molecular abstraction of hydrogen and the subsequent addition of O₂ comprising the autoxidation channel (Bianchi et al., 2019) are represented by Reaction (R5a).

$$\begin{array}{}\text{(R5a)}& {\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\stackrel{\text{H-shift}}{⟶}{\mathrm{RO}}_{\mathrm{2}}^{\prime }\mathrm{•}\end{array}$$

In cases where the abstracted H is in the α-position of a hydro(pero)xy functional group, a carbonyl group is formed to terminate the autoxidation (Reaction R5b; Orlando and Tyndall, 2012).

$$\begin{array}{}\text{(R5b)}& {\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\stackrel{\text{H-shift}}{⟶}\mathrm{RC}=\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}\end{array}$$

Any molecular rearrangements leading to the fragmentation of the carbon chain are represented by Reaction (R5c).

$$\begin{array}{}\text{(R5c)}& {\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\stackrel{\text{H-shift}}{⟶}\text{fragmentation products}\end{array}$$

Due to their relatively short lifetimes (at most, 1 ms in the lower atmosphere; Orlando et al., 2003) and resulting low concentrations, bimolecular reactions (except for O₂ addition upon autoxidation) of alkoxy radicals are neglected in the current approach. Analogous to RO₂•, RO• can undergo autoxidation along with the same competing channels (Bianchi et al., 2019; Vereecken and Peeters, 2010).

$$\begin{array}{}\text{(R6a)}& {\displaystyle }\mathrm{RO}\mathrm{•}\stackrel{\text{H-shift}}{⟶}{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}\text{(R6b)}& {\displaystyle }\mathrm{RO}\mathrm{•}\stackrel{\text{H-shift}}{⟶}\mathrm{RC}=\mathrm{O}+\mathrm{OH}\mathrm{•}\text{(R6c)}& {\displaystyle }\mathrm{RO}\mathrm{•}\to \text{fragmentation products}\end{array}$$

Note that the rearrangement of the alkoxy radical (roughly 10³ to 10⁷ s⁻¹) is considered to happen much faster compared to the peroxy radical (mainly below sub-seconds, with few exceptions) (Crounse et al., 2013; Praske et al., 2018; Vereecken and Nozière, 2020; Vereecken and Peeters, 2010).

The concentrations of the (un-fragmented) carbon-centred radicals and their closed-shell reaction products are obtained from ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS measurements. However, there are other species in Reactions (R1)–(R6) that require different determination methods. In the present work, the concentrations of HO₂•, NO•, and ΣRO₂• (including all peroxy radicals of the chemical system) are determined by modelling. The MCM, which describes the tropospheric degradation of a variety of hydrocarbons, is deployed for this purpose. Concentrations of fragmentation products, due to the unknown fragmentation pathways, are estimated (RO reaction branch; the lower limit is 0, and the upper limit is determined by the kinetic limitation for the considered reaction, e.g. RO₂+HO₂; for Reaction R6c, the upper limit is the production of RO species).

To greatly simplify the solution of the mathematical description of the autoxidation chemistry, we consider a well-mixed steady-state system (there is no timely variation in the ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS signals). As a result, the differential equations governing the evolution of the chemical species are reduced to differences that can be represented by linear equations:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}C}{\mathrm{d}t}}\approx {\sum }_i{\displaystyle \frac{\mathrm{\Delta }{C}_i}{\mathrm{\Delta }t}}=\mathrm{0},\end{array}$$

where i is the number of processes impacting the concentration (C) of a chemical species. A similar experimental setup was investigated by Roldin et al. (2019) to derive rate coefficients for an autoxidation chemistry scheme. The procedure of rate fitting to reproduce the mass peaks detected by CIMS represents a considerable workload (several weeks to months for a single VOC system). In the present work, we approach the problem differently to enable automation: instead of incrementally optimising rate coefficients to meet a mass peak distribution at a certain point in time, we set up the linear set of equations describing the steady state. Each solution of the set of linear equations represents a valid mathematical solution to the problem (i.e. a set of reaction rate coefficients explaining the CIMS measurement). The recently published automated alkoxy-radical or peroxy-radical autoxidation mechanism framework (autoAPRAM-fw; Pichelstorfer et al., 2024) is capable of creating autoxidation reaction schemes in an automated fashion for any VOC system. Due to the large number of equations involved and the potentially numerous solutions, we apply the autoAPRAM-fw to create a description of the autoxidation chemistry (without assigning rate coefficients): the “APRAM scheme”. Briefly, the framework uses input peroxy radical names, their atomic compositions and the information on the reaction types considered to create a list of reactions, including product names (with their likely atomic compositions) and default reaction rate coefficients. For details on the formalism, we refer the reader to the original article.

Consideration of the physical boundary conditions of the experimental configurations (wall interaction, influx and outflux) allows the linear set of equations relating changes in the detected mass peak to the chemical change terms (obtained from the reaction scheme) to be constructed. The unknowns (k) represent the missing rate coefficients:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{\Delta }C(\mathrm{CHON}{)}_x}{\mathrm{\Delta }t}}& ={\sum }_{{\mathrm{CHON}}_i={\mathrm{CHON}}_x}{\displaystyle \frac{\mathrm{\Delta }{C}_i}{\mathrm{\Delta }t}}\\ & ={\sum }_{m,n\to i}{k}_m\times \left[{\mathrm{R}}_{\mathrm{1},m}\right]\times \left[{\mathrm{R}}_{\mathrm{2},n}\right]\\ & +{\sum }_{u\to i}{k}_u\times \left[{\mathrm{R}}_u\right]\\ & -{\sum }_i{\displaystyle \frac{\mathrm{\Delta }{C}_{i,\mathrm{phys}}}{\mathrm{\Delta }t}},\end{array}\end{array}$$

where ΔC(CHON)_x is the change in concentration per cubic centimetres of CIMS-detected species with atomic composition CHON. For each experimentally determined atomic composition, a list of model isomers i and related concentration changes ΔC_i can be assigned. This list may be empty in case the chemical scheme does not cover the experimentally determined species. The first term on the right-hand side of Eq. (1) represents all changes to the related chemical scheme product's isomer concentration (rate coefficient k and reactants R₁ and R₂) due to bimolecular reactions. The second term represents unimolecular reactions and the third term summarizes any physical changes to the scheme products' concentrations C_i (i.e. a dilution flow in the present work). A detailed description of how Eq. (2) is set up and solved for each species of the observed spectrum can be found in the supporting information.

2.1 Key aspects of the approach

2.1.1 RO₂•

Clearly, the peroxy radical is a key species in the description of the autoxidation chemistry (Ehn et al., 2014; Goldman et al., 2021). As a result, determination of the RO₂• abundance is an important task in constraining the chemistry. In the present work, we use simulated data mimicking the ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS experimental data to derive the RO₂• concentrations. In experimental applications, it is assumed that all highly oxygenated RO₂• species are quantified with equal sensitivity (Hyttinen et al., 2018).

2.1.2 RO•

Alkoxy radicals, owing to their short lifetimes (roughly 0.1 ms in Earth's atmosphere; Orlando et al., 2003), are not measured and, accordingly, are not a target of the reaction rate analysis. Instead, the fraction of reaction products branching towards the alkoxy is estimated (Reactions R2c, R3b and R4c). Similarly, the reaction product branching of Reaction (R6) is estimated in order to investigate the potential effects of the alkoxy pathways on the RO₂• abundance and closed-shell species formation. The RO• chemistry (a) allows the RO₂• oxygen amount to switch between odd and even numbers and (b) enables the autoxidation to proceed effectively at low RO₂• concentrations via Reactions (R2c), (R3b) or (R4c), followed by Reaction (R6a).

2.1.3 Closed-shell species

Setting up the (chemical) formation and (physical) loss balance for closed-shell species allows for the determination of rate coefficients applied in reaction types (Reactions R1, R2a–b, R3a, R4a–b, R5b, and R6b).

2.1.4 Fragmentation products

Although direct inclusion of reactant-specific fragmentation products is beyond the scope of this work, the effect of this reaction can be investigated. For mass balance, the larger the estimated flux through fragmentation (see Reactions R2d, R3c, R4d, R5c and R6c), the higher the production of the reagents via Reactions (5a) and (6a) must be. Accordingly, the fragmentation branching has a potentially large impact on the H-shift rates determined with the suggested method.

2.1.5 H-shift rates

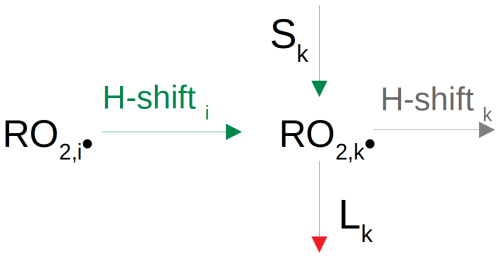
Deriving H-shift rates requires determination of the CS-forming rate coefficients, estimation of the loss through fragmentation reactions and calculation of potential contributions via alkoxy pathways. RO₂• H-shift rates leading to the formation of another RO₂• species with an oxygen atom number raised by 2 (i.e. reaction type 5a – autoxidation) can be calculated from a balance equation (see also Fig. 1):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{\Delta }C\left({\mathrm{RO}}_{\mathrm{2},k}\mathrm{•}\right)}{\mathrm{\Delta }t}}=\\ & k_{\text{H-shift}}C\left({\mathrm{RO}}_{\mathrm{2},i}\mathrm{•}\right)S_k-L_k-k_{\text{H-shift}}C\left({\mathrm{RO}}_{\mathrm{2},k}\mathrm{•}\right),\end{array}\end{array}$$

where C(RO_2,k•) is the concentration of the peroxy radical k. S_k is a source term considering all potential contributions, including wall sources, autoAPRAM-RO• autoxidation and MCM-RO• and MCM-RO₂• pathways. L_k is a loss term (physical as well as chemical but not including RO₂• autoxidation). RO_2,k• is the product of RO_2,i• undergoing H-shift and O₂ addition.

Figure 1 Balance of the influx and outflux of RO_2,k• to derive the H-shift rate for RO_2,i•.

The determination of H-shift reaction rate coefficients of RO_2,i• forming RO_2,k• requires (a) knowledge of closed-shell and fragmentation species formation rate coefficients and (b) the H-shift rate of the RO_2,k•. Accordingly, Eq. (2) is solved starting with the closed-shell species of the largest molecular mass (more information on this can be found in the Supplement – “On sorting the input CIMS data”). Next, fragmentation and alkoxy pathways are considered, enabling the H-shift rate to be assigned.

2.2 The effect of RO₂• species not part of the APRAM scheme

In the present work, the autoxidation chemistry scheme is created by the autoAPRAM-fw. It does not include the degradation of the VOC upon oxidation, except for a few reactions resulting in fragmentation of the reactant (Reactions 3c, 4d, 5c and 6c). If autoxidation products from the autoAPRAM-fw were to comprise a small fraction of the total abundance of RO₂•, reactions with ΣRO₂• may be dominated by species outside the autoxidation scheme, depending on their reaction rates. This potential dominance is neither guaranteed nor obvious, as the respective reaction rate coefficients may be 1 or 2 orders of magnitude different for the RO₂• formed by the fragmentation of the carbon chain or oxidation of a different parent VOC (Jenkin et al., 2019). Knowledge of the abundance of non-APRAM RO₂• is required to equip the ΣRO₂• reactions with rate coefficients. Further, the lowest oxygen number containing species considered by the autoAPRAM-fw may not be formed within the framework. Accordingly, the present approach requires a model describing the degradation of the VOC (i.e. oxidation reactions leading to fragmentation of the VOC carbon chain, ultimately forming CO₂). This process is characterised by a sequence of oxidation reactions forming radicals (R•, RO• and RO₂•) that decompose or form closed-shell species. Some of these radicals may undergo autoxidation, thereby forming species considered by the APRAM chemical scheme. In the present work, MCM serves to degrade the VOC, creating radicals and estimating concentrations of RO₂• (i.e. species that are not considered in the APRAM scheme). Here, MCM forms the enabling assumption for solving the chemical equations.

To estimate the flux from a specific (MCM) species into the APRAM scheme, the consumption of the product peroxy radical RO_2,k• (by dilution, wall loss and chemical reactions) is balanced with potential formation terms (see Fig. 1). In cases where H-shift of RO• and RO_2,i• (both part of the autoxidation scheme) may not compensate for the consumption of RO_2,k, additional production terms are required. In particular, at the lower molecular mass end of the mass spectrum (where no RO_2,k formation reactions via the autoAPRAM scheme exist), the consumption of a radical has to be balanced entirely by an influx. Determination of the required influx is made possible by the order of calculation: as presented in the methodology, the scheme is equipped with rate coefficients starting at the upper observed product mass, as explained in the next section (“Solving the equations”). In the final step, a required influx may be calculated as described below (molec. cm⁻³ s⁻¹).

In the present autoxidation chemistry, the production flux of RO_2,k• can originate from (a) RO• and RO₂• undergoing autoxidation as well as (b) production of species by reactions not covered by the autoxidation chemistry. The initiation flux probability (P) via the RO• and RO_2,i• pathways to balance the loss of RO_2,k• is considered.

$$\begin{array}{}\text{(4)}& {\displaystyle }P\left(\mathrm{RO}\mathrm{•}\right)=\mathrm{1}-{\displaystyle \frac{\left(L_{\mathrm{chem}}+L_{\mathrm{phys}}-S_{\mathrm{in}}\right)}{\left(L_{\mathrm{chem}}+L_{\mathrm{phys}}+S_{\mathrm{in}}\right)}},\text{(5)}& {\displaystyle }P\left(\mathrm{RO}{\mathrm{•}}_{\mathrm{2},i}\right)=\mathrm{1}-{\displaystyle \frac{\left(C\left({\mathrm{RO}}_{\mathrm{2},i}\right)k_{\mathrm{autox},\mathrm{high}}\right)}{\left(L_{\mathrm{chem}}+L_{\mathrm{phys}}-S_{\mathrm{in}}\right)}}\end{array}$$

L are the chemical (“chem”) and physical (“phys”) loss terms of RO_2,k• (see Fig. 1 for the relations RO_2,i• and RO_2,k•). S_in is a source term of RO_2,k• via the alkoxy pathway. C(RO_2,i) is the concentration of RO_2,i• and k_autox,high is a (structure-independent) estimated upper limit for the autoxidation rate of RO_2,i•. In the current work, we assumed k_autox,high = 2 s⁻¹. We chose this conservative upper limit as most H-shifts are significantly slower, although considerably higher H-shift rates have been reported in the recent literature (Iyer et al., 2023). The initiation flux probabilities of RO• and RO₂• relate to Eq. (3) as all are based on considerations of mass conservation. While Eq. (3) explicitly balances mass fluxes, P is meant to highlight the imbalances in fluxes by considering (a) mass fluxes via the RO pathway for P(RO•) and (b) expected limitations of the fluxes from RO₂• within the autoAPRAM scheme for P(RO₂•).

Where probabilities P(RO•) and P(RO₂•) both approach 1, an initiation flux to compensate for the loss of RO_2,k• is very likely required. The magnitude of the influx can be determined as the difference between the loss of RO_2,k• and the formation via RO• and RO_2,i• paths.

Where the probabilities P(RO•) and P(RO₂•) are both ≪ 1, influx is not a prerequisite but is still possible. P(RO•) and P(RO₂•) are defined in the range [0;1]. Negative results indicate a likely initiation flux for P(RO•) and an unlikely initiation for P(RO₂•). In this case, H-shifts of RO• and RO₂•, together with the initiation flux, form an equation with three unknowns. Accordingly, the potential solution space is a 2-D surface. Calculated influx probabilities for all of the RO₂• species considered can be found in the Supplement (Table S2).

2.3 Solving the equations

Rate coefficients are assigned by applying the newly created and semi-automated autoCONSTRAINT tool (Fig. 2). The autoCONSTRAINT tool reads in a chemical scheme with no rate coefficients, together with a mass spectrum obtained e.g. with ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS. The ΣRO₂•, HO₂• and NO• concentrations as well as the boundary conditions (temperature, wall loss and dilution) are additionally required as input parameters.

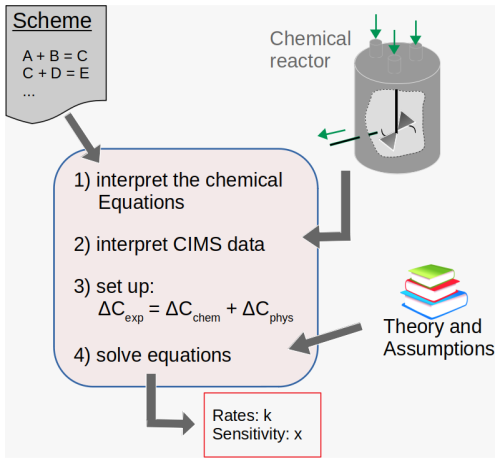
Figure 2 The autoCONSTRAINT workflow. The autoCONSTRAINT module reads in chemical schemes and experimental results (including high-resolution CIMS data). The typically under-constrained equations are solved by adding theoretical knowledge or assumptions. The output covers rate coefficients k and an estimate of their sensitivity x.

Based on the autoAPRAM scheme, autoCONSTRAINT derives the linear set of equations (i.e. Eq. 2) describing the chemical and physical change terms for the ${\mathrm{NO}}_{\mathrm{3}}^{-}$ CIMS-detected peak list. Note that not all peaks detected with CIMS may be covered by the scheme. Analogously, not all of the species from the APRAM scheme may be detected with CIMS. In both cases, a rate coefficient related to these species is not accessible.

Typically, each CIMS-detected peak relates to several change terms (production and loss reaction pathways). Consequently, there are several unknowns, as every chemical change term of Eq. (2) features a rate coefficient. To enable solutions for the rate coefficients, the number of unknowns is reduced by providing a guess at the relative magnitudes of the rate coefficients. For example, in the case of the three unknown rate coefficients, an estimate for two of them in relation to the third must be provided. As a result, the solutions are typically not unique. However, where they are chemically meaningful (i.e. the rate coefficients are in the interval from 0 to the kinetic or theoretical limit), they represent a pool of equally valid solutions. Provision of relative values for rate coefficients can account for both experimental and theoretical findings.

A detailed description of the construction and solution of Eq. (2) for each species of the observed spectrum can be found in the supporting information (note that the mass spectrum input may also be of a simulated nature and does not necessarily have to be experimental).

Equation (3) depicts the dependence of the H-shift rate of a species i on the loss terms of RO_2,k• (which is increased in mass by two oxygen atoms). Consequently, determination of the rate coefficients starts at the upper end of the mass spectrum. This enables the chemical consumption of every RO₂• species to be determined before the autoxidation rates are calculated. A detailed depiction of these considerations can be found in the Supplement (section “On sorting the input CIMS data”).

We examined modelled data to showcase the ability of autoCONSTRAINT to reproduce rate coefficients from an input chemistry scheme. For this demonstration, a scheme mimicking the autoxidation of α-pinene was created (i.e. the αpin-test scheme) by applying the autoAPRAM-fw. The full scheme can be found in the supporting data (PyCHAM/input/apinene_autoPRAM_V01_scheme.dat). Roldin et al. (2019) provided a possible solution for the same chemical system in a similar autoxidation scheme. However, the species covered in the present approach do not fully match those covered by Roldin et al. (2019). The difference is the description of the adduct formation: in the work of Roldin et al. (2019), the adduct formation is lumped, while it is specific to reagent products in the αpin-test scheme. As a result, the scheme presented in this work should be considered fully independent of the Roldin et al. (2019) scheme, and its sole purpose is to create data to be analysed using autoCONSTRAINT. The reason for choosing α-pinene is to illustrate the model's potential to deal with systems of similar complexity.

We followed the steps described in Fig. 2 to apply the method:

• 1.

  The αpin-test scheme (without rate coefficients) describing α-pinene autoxidation was inputted into autoCONSTRAINT, and the reactions are interpreted. Optionally, the model reports the read-in reactions and how they are interpreted (see the file “chem_interpretation.txt” in the Supplement).

• 2.

  To mimic “experimental data”, the PyCHAM model (O'Meara et al., 2021) simulations were conducted in flow reactor mode (i.e. there are inflows and outflows to the chamber, with characteristic residence times and losses by dilution). Details of the simulation setup can be found in the Supplement (section “PyCHAM inputs”). The point in time for analysing the change in the CIMS signal was chosen 6 h after the start of the simulation. At this time, the chemical system can be approximated as being in a steady state. The PyCHAM model results, which include full information on the isomeric distribution, were converted into a high-resolution CIMS data format (i.e. the data include information on the atomic composition only, and therefore isomers cannot be distinguished) and provided as input into autoCONSTRAINT. Additional (simulated) data used in the analysis describe the concentrations (and change rates) of species not part of the αpin-test scheme (see Sect. 2.2 for more information).

  After sorting the CIMS peaks in descending mass order, species from the αpin-test scheme were assigned to their respective mass spectrum peaks based on their atomic composition. This allows assembly of the chemical and physical change terms for each peak in the mass spectrum (examples can be found in the Supplement – section “Exemplary solution of equ. (2)”).

• 3.

  MCM simulations of α-pinene oxidation were conducted to provide an estimate of the peroxy radical isomeric distribution of species not covered by the αpin-test scheme, in addition to estimates of the concentrations for NO•, HO₂• and ΣRO₂• (since these quantities were not measured in this example).

• 4.

  The equations were solved after providing an estimate of the relative magnitudes of the individual reaction types' rate coefficients. The relative values applied were provided as an input.

3 Results and discussion

3.1 Reproduction of k rates from a known scheme

The reproduction of rate coefficients from the αpin-test scheme is summarised in Fig. 3 and Figs. S4–S7. The deviation from the αpin-test scheme rate coefficients is below 0.2 % for all rate coefficients except for accretion products, which show a maximum error of 0.57 % and a mean absolute error of 0.05 %.

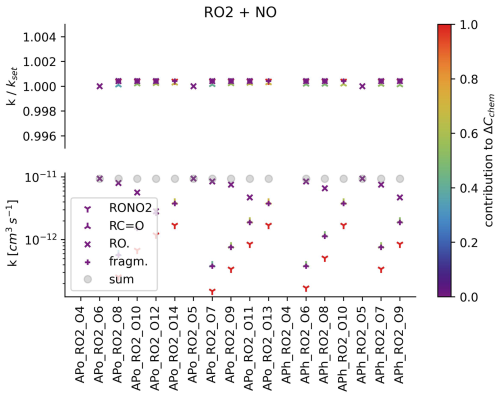
Figure 3 RO₂ radicals (names are given by the abscissa) react at a rate (denoted as the lower ordinate) to form RONO₂ (downward-facing triangle), alkyl species (upward-facing triangles), fragmentation species (plus) and alkoxy radicals (crosses). The sum of the individual reaction channel's rates is shown by a circle. The precision of rate coefficient recovery from the (simulated) mass spectrum is shown as the upper ordinate. The colour code denotes the calculated contribution of the reaction to the change (by means of chemical reactions) in the CIMS mass peak concentration.

Based on the choice of the relative magnitude of the individual rate coefficients, the contribution of a single reaction to the sum of the chemical changes can be determined. An example is given in the Supplement (see section “Setting up equ (2) for mass peak 214”). As the contribution decreases, the dependence on the choice of relative rate coefficient increases. For example, reaction channel A contributes 99 % of the chemical changes in an observed product, and reaction channel B contributes 1 %. When doubling the contribution of reaction B, its rate roughly doubles but the rate of reaction A remains almost the same (changing by roughly 1 %). Accordingly, the colour code in Fig. 3 can be interpreted as a sensitivity parameter.

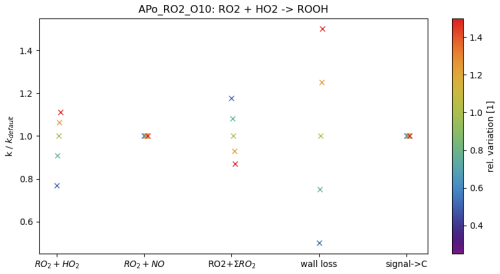
Figure 4 presents an example of the impact of the estimate of relative rate coefficients on an estimated rate coefficient (in this example, the rate coefficient of RO₂•(Apo_RO2_O10) + HO₂•→ROOH). The parameter of interest (see the abscissa) is varied by −50 %, −25 %, +25 % and +50 %, as indicated by the colour bar. The variation of the guess for Reaction (R3a) (i.e. ${\mathrm{RO}}_{\mathrm{2}}\mathrm{•}+{\mathrm{HO}}_{\mathrm{2}}\mathrm{•}\to \mathrm{ROOH}$) results in a change in the rate coefficient of −23 % to +11 %. The guess in Reaction (R4) (RO₂•+NO•) does not affect the product ROOH. For the variation of Reaction (R2) (RO₂•+ΣRO₂•), an indirect effect on Reaction (R3a) is observed. Reduction of the guess value by 50 % results in an increase in k_ROOH of roughly 18 %, while increasing the guess for Reaction (R2) by 50 % reduces the k_ROOH by 17 %. The wall loss has a direct effect on the rate coefficient k_ROOH: changing the estimate of the wall loss by a given amount results in a similar change in the rate coefficient. Assuming that the conversion from the CIMS signal to the concentration can be approached by a constant value (i.e. uniform sensitivity of the instrument) for all molecules of the autoAPRAM reaction scheme, there is no effect of this constant value on the rate coefficient k_ROOH. However, the conversion constant affects the reactions that involve RO₂•-${\mathrm{RO}}_{\mathrm{2}}^{\prime }\mathrm{•}$ reactions forming adducts (Reaction R1), carbonyls (Reaction R2b) or alcohols (Reaction R2a) due to the square dependence on the RO₂• concentrations: in the other reactions (bimolecular or unimolecular) considered in this work, a single reagent (RO₂•) and the product are sampled with a certain sensitivity. Consequently, this sensitivity, if uniform, does not matter as long it is high enough to detect the peaks properly. The potential reaction partners (NO• and HO₂•) are not subject to this sensitivity as they are determined by other means. However, where both reagents (RO₂• and ${\mathrm{RO}}_{\mathrm{2}}^{\prime }\mathrm{•}/\mathrm{\Sigma }{\mathrm{RO}}_{\mathrm{2}}\mathrm{•}$) are subject to this sensitivity, the product-forming rate coefficient is linearly dependent on it.

Figure 4 Effect of variation of the rate coefficient guess (RO₂•+HO₂•, RO₂•+NO• and RO₂•+ΣRO₂•), the “wall loss” and the signal-to-concentration conversion (“signal → C”) on the formation of ROOH species via Reaction (R3a). The colour bar indicates the magnitude of the variation of the guess.

3.2 Interpretation of the result

All results determined with the proposed method, mathematically, represent a valid solution (i.e. a full set of rate coefficients for the scheme) to the problem. Several of the solutions found may satisfy the boundary conditions (e.g. the rate coefficient may not exceed the kinetic limit). These are all mechanistically plausible, and there is no additional constraint available to determine which of the solutions is the best. To discriminate between them, additional information is required. As the mathematical nature of the drafted approach is a linear set of equations, additional information can be obtained by considering multiple sets of CIMS data determined under different chemical regimes.

3.3 On determining multi-experiment-based realistic rate coefficients

The confidence in the calculated rate coefficients is dependent on the corresponding reaction's dominance among the chemical terms in Eq. (2). For example, we can determine with confidence the rate of the reaction RO₂•+HO₂• when the product, ROOH, comprises a large share of the product isomers. As discussed in Sect. 3.1, “Reproduction of k rates from a known scheme”, the value of the rate coefficient is only weakly dependent on the choice of relative k if the reaction channel is dominant. As a result, data from an experiment covering just one point in the chemical space provide a relatively poor constraint over rate coefficients for minor reactions at that point. Consequently, datasets gathered under a range of chemical regimes (high HO₂•, high NO_x, high RO₂• and low NO_x) can be jointly analysed to more effectively quantify all rate coefficients.

The chemistry under investigation is clearly complex, and the proposed approach, likely, will never cover all reaction channels and species. However, we show that plausible solutions can be inspected using the autoCONSTRAINT method in order to provide mechanistic insight and to quantify the most likely rates of much of the dominant chemistry in the system. The larger the number of experiments and the broader the coverage of the chemical space, the greater the confidence in the rate coefficients determined by the approach.

As the method is, as yet, unable to solve the rate coefficients from several datasets simultaneously, they are determined one by one. To find a “good” set of rate coefficients, relative rate coefficients must be found that work for each dataset. To overcome this problem, an algorithm to search the parameter space of the relative rate coefficients is in development. Where the types of chemical equations represent a good description of the dynamics in the system, at least one region in the parameter space of relative k rates can be found, reporting similar rate coefficients from all experiments. Note that these rate coefficients are ideally determined from dominant reaction terms (Eq. 2).