Cluster-to-particle transition in atmospheric nanoclusters

The formation of molecular clusters is an imperative step leading to the formation of new aerosol particles in the atmosphere. However, the point at which a given assembly of molecules represents an atmospheric molecular cluster or a particle remains ambiguous. Applying quantum chemical calculations, we elucidate this cluster-to-particle transition process in atmospherically relevant sulfuric acid–base clusters. We calculate accurate thermodynamic properties of large (SA)_n(base)_n clusters (n=1–15), with SA being sulfuric acid and the base being either ammonia (AM), methylamine (MA), dimethylamine (DMA) or trimethylamine (TMA). Based on our results, we deduce property-based criteria for defining freshly nucleated particles (FNPs), which act as a boundary between discrete cluster configurations and large particles. We define the onset of FNPs as being when one or more ions are fully solvated inside the cluster and when the gradient of the size-averaged binding free energy approaches zero. This definition easily allows the identification of FNPs and is applicable to particles of arbitrary chemical composition. For the (SA)_n(base)_n clusters studied here, the cluster-to-particle transition point occurs around 16–20 monomers.

We find that the formation of FNPs in the atmosphere depends greatly on the cluster composition and atmospheric conditions. For instance, at low temperature (278.15 K) and high precursor concentration (AM =10 ppb and MA =10 ppt), the SA–AM and SA–MA systems can form clusters that grow to and likely beyond ∼ 1.8 nm sizes. The SA–DMA system forms clusters that grow to larger sizes at low temperature (278.15 K), independent of the concentration (DMA =1–10 ppt), and the SA–TMA system (1:1 acid–base ratio) can only form small clusters that are unable to grow to larger sizes under the studied conditions.

1 Introduction

The recent 2023 Intergovernmental Panel on Climate Change (IPCC) report verifies that aerosol–cloud interactions remain the largest uncertainty in global radiative forcing (Lee et al., 2023). New particle formation (NPF) processes are believed to account for up to half of the number of cloud condensation nuclei (Merikanto et al., 2009). The formation of new aerosol particles occurs through nucleation of gas-phase vapors (Kulmala et al., 2013). Initially, small molecular clusters are formed via strong intermolecular interactions between atmospheric vapor molecules. Under the premise that these clusters do not evaporate or are lost due to coagulation with existing particles, they can grow to larger sizes, eventually becoming aerosol particles over 2 nm in diameter, which is the detection limit of many standard atmospheric measurement sites, while smaller particles require mass spectrometer and condensation particle counter techniques.

Sulfuric acid (SA) has unequivocally been shown to be a prime driver of NPF over land and the oceans (Sipilä et al., 2010). However, base molecules are required to facilitate the cluster formation process in the lower troposphere (Kirkby et al., 2011). Highly abundant bases with low basicity, such as ammonia (AM) or less abundant but more basic alkylamines such as methylamine (MA), dimethylamine (DMA) and trimethylamine (TMA), have been confirmed to participate in the cluster formation process. The seminal work by Kurtén et al. (2008) showed that the strong binding of less abundant but stronger bases (such as DMA) could overshadow the effect of more abundant but less strong bases such as ammonia in the initial clustering process with SA. This was reaffirmed in the state-of-the-art CLOUD chamber experiments by Almeida et al. (2013).

Jen et al. (2014) studied the stabilization of sulfuric acid dimers by AM and alkylamines (MA, DMA and TMA) using a flow tube reactor setup. At SA concentrations in the range of 10⁷–10⁹ molec. cm⁻¹ and base concentrations leading to saturated SA dimer concentrations, the following trend of dimer stabilization was identified: AM < MA < TMA ≤ DMA. Glasoe et al. (2015) expanded on the work of Jen et al. (2014) by studying 1.8 nm sulfuric acid–base particle formation. Here an AM < MA < DMA < TMA trend was found. These studies imply that both the initial cluster formation rates and 1.8 nm particle formation rates are highly dependent on the basicity of the bases. Elm (2021a) studied small (SA)₁₋₂(base)₁₋₂ cluster formation using computational methods and found a similar trend in the cluster formation potential. Computational work by Kubečka et al. (2023b) showed that TMA is involved in the initial SA–base cluster formation process, but larger clusters with more than one or two TMA molecules are unstable, making TMA evaporate. However, the presence of TMA could still contribute to NPF, increasing the nucleation rate by ∼ 50 % at 298.15 K. This mechanism has been confirmed as occurring in polluted environments, such as the urban Beijing atmosphere, where SA–base clusters with up to one TMA molecule were detected using a chemical ionization–atmospheric pressure interface–time-of-flight (CI-APi-TOF) mass spectrometer (Cai et al., 2023). Composition-wise, both computational studies (Olenius et al., 2013; Elm, 2017) and experimental results (Kürten et al., 2014) have shown that SA–base cluster formation is most favourable when there is a 1:1 ratio of acids to bases, with the limiting step being the initial formation of the (SA)₁(base)₁ clusters (Elm, 2017; Cai et al., 2022).

Following the cluster formation process from single molecules up to measurable ∼2 nm particle sizes was previously not directly possible for electrically neutral clusters using either experimental or computational techniques. Quantum chemical calculations can be applied to calculate accurate thermochemistry of the clustering process, thereby giving direct information on the relative importance of different clustering species. However, such accurate calculations are computationally expensive and can only routinely be performed on clusters containing up to a maximum of eight monomers (see recent comprehensive reviews: Elm et al., 2020, 2023; Engsvang et al., 2023b). We recently pushed this limit by studying large (SA)_n(AM)_n clusters, with n=1–30 (Engsvang and Elm, 2022; Engsvang et al., 2023a). To study such large systems, we had to reduce the level of theory and were limited to GFN1-xTB (Grimme et al., 2017) geometries and B97-3c (Brandenburg et al., 2018) single point energies. However, we identified large uncertainties in the calculated thermochemistry, which was ascribed to insufficient configurational sampling (Engsvang and Elm, 2022; Engsvang et al., 2023a). We recently addressed this issue and found that several parallel configurational sampling runs yielded the most reliable final configurations. Hence, we now have a computational methodology that can be applied all the way from single molecules to (SA)_n(base)_n clusters of sizes up to ∼ 2 nm.

Here, we further explore the chemical complexity of large clusters by studying (SA)_n(base)_n clusters (n=1–15), with SA being sulfuric acid and the base being either AM, MA, DMA or TMA. Based on the results, we will deduce a property-based criterion to define when a given assembly of molecules represents an atmospheric molecular cluster or a freshly nucleated particle (FNP).

2 Methods

2.1 Computational details

Density functional theory calculations employing the empirically corrected B97-3c (Brandenburg et al., 2018) method were performed in ORCA 5.0.4 (ORC, 2012). In the case of the (SA)₁₄(TMA)₁₄ system, we had to apply a VeryTightSCF criterion to ensure convergence. Semiempirical tight binding calculations were performed using the original GFN1-xTB (Grimme et al., 2017) model and a re-parameterized GFN1-xTB model, denoted as GFN1-xTB^re-par (see the next section). The calculations were performed in the XTB program (Bannwarth et al., 2021), version 6.4.0.

Cluster configurational sampling based on the artificial bee colony (ABC) algorithm was performed with the ABCluster program (Zhang and Dolg, 2015, 2016) using a CHARMM force field. Additional configurational sampling was performed with CREST 2.12 (Grimme, 2019; Pracht et al., 2020, 2024). All the calculations and data collections were performed with the freely available JKCS/JKQC suite of scripts (Kubečka et al., 2023a).

2.1.1 Cluster configurational sampling

Here we study (SA)_n(base)_n clusters, with n=1–15 and bases AM, MA, DMA and TMA. The SA–AM and SA–DMA systems were previously explored by Wu et al. (2023), and additional sampling was carried out with CREST in this work.

Configurational sampling techniques of small (n≤4) atmospheric (SA)_n(base)_n clusters are well established in the literature (Temelso et al., 2018; Kubečka et al., 2019; Odbadrakh et al., 2020). However, sampling large clusters with n≥5 presents an enormous challenge. To thoroughly explore the configurational space of the clusters, we apply our recently identified configurational sampling workflow, which has been optimized towards sampling of large cluster structures (Wu et al., 2023):

$$\begin{array}{c}{\displaystyle }\mathrm{\text{ABC}}\stackrel{N=\mathrm{10}\mathrm{000}}{⟶}{\text{xTB}}^{\text{OPT}}\stackrel{N=\mathrm{10}\mathrm{000}}{⟶}{\text{B97-3c}}^{\text{SP}}\\ \text{(ABC track)}& {\displaystyle }\underset{\text{filter}}{\stackrel{N=\mathrm{1000}}{⟶}}{\text{B97-3c}}^{\text{PART OPT}}\underset{\text{filter}}{\stackrel{N=\mathrm{100}}{⟶}}{\text{B97-3c}}^{\text{FULL OPT}}.\end{array}$$

Briefly, 10 separate configurational sampling explorations are performed with the ABCluster program (SN =1280, gen =320, sc =4), saving the 1000 lowest minima for each run. Ten parallel runs should be sufficient to model clusters consisting of up to 15 acid–base pairs (Wu et al., 2023) but might be excessive for the smallest clusters studied here. However, we kept the number of runs constant for simplicity. Ionic monomers were used in all the sampling runs. Each generated configuration is then optimized at the GFN1-xTB level of theory. A B97-3c single point energy is calculated on top of all the GFN1-xTB structures, and the 1000 structures lowest in electronic energy are subsequently partially optimized with 4n iterations for the (SA)_n(base)_n systems at the B97-3c level. Finally, the 100 structures lowest in electronic energy based on the partial optimization are fully optimized, and vibrational frequencies are calculated at the B97-3c level of theory.

The identified clusters were used to re-parameterize GFN1-xTB with the same methodology as Knattrup et al. (2024), where the error of the electronic binding energies and gradients are minimized between GFN1-xTB and B97-3c. The three configurations with the lowest electronic energy in (SA)_n(AM/MA/DMA/TMA)_n clusters ($n=\mathrm{1}-\mathrm{15}$) from ABC track were used as the optimization set. This leads to an optimization set comprising a total of 179 clusters. The GFN1-xTB re-parameterization based on this optimization set will be denoted as GFN1-xTB^re-par. To further explore the vast configurational space of these large clusters, the identified cluster structure lowest in free energy at the B97-3c level from the ABC track is additionally used as input for sampling with CREST using the newly parameterized GFN1-xTB. Hence, we employed the following “improvement workflow” as given by Knattrup et al. (2024):

$$\begin{array}{}\text{(CREST track)}& {\mathrm{\text{CREST(GFN1-xTB}}}^{\text{re-par}})\stackrel{N=\mathrm{100}}{⟶}{\text{B97-3c}}^{\text{FULL OPT}}.\end{array}$$

The CREST simulations were run in non-covalent interaction mode (–nci) with the GFN1-xTB^re-par model, and we employed an energy window of 30 kcal mol⁻¹ (–ewin 30). We emphasize that, while this overall workflow (ABC and CREST track) can very accurately identify low free energy configurations of large clusters, it is also extremely demanding computationally. However, we note that one can never be certain of locating the global minimum.

The final structures from the ABC and CREST sampling tracks are merged, and unique configurations are identified based on a root mean squared deviation (RMSD) using the ArbAlign program (Temelso et al., 2017), with an RMSD cutoff of 0.4 Å. As the largest studied system – (SA)₁₅(TMA)₁₅ – contains 300 atoms, the changes in hydrogen atom positions will mask the changes in the more relevant atoms by averaging over atoms with RMSD. Hence, during the uniqueness test, we compared the geometries containing only sulfur and nitrogen atoms, and thereby local structure variations will be neglected. For instance, the rotation of a methyl group or the bending N–C–H angle does not contribute to the RMSD value.

2.1.2 Free energies

We calculate the binding free energies as the free energy of the cluster with respect to its individual monomers:

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{G}_{\text{bind}}=G_{\text{cluster}}-\sum _i{G}_{\text{monomers},i}.\end{array}$$

We also calculate the size-averaged binding free energies ($\mathrm{\Delta }{G}_{\mathrm{bind}}/m$) of the clusters as the physical interpretation is the binding free energy contribution per monomer in the cluster. This quantity provides insight into the average binding properties of the cluster and offers inferred evidence of the thermochemistry associated with monomer addition. Analyzing how the average binding free energy changes with cluster size will present us with the stabilization processes occurring during cluster growth. A recent work by Sindel et al. (2022) used a similar definition to study TiO₂ clustering, leading to a convergence of the size-averaged binding free energies to the formation free energy of the bulk crystal. For example, consider the difference in the average binding free energy between a (SA)₉₉(AM)₉₉ cluster and a (SA)₁₀₀(AM)₁₀₀ cluster. In such large clusters, adding one extra acid–base pair results in minimal molecular rearrangement, and thus the average binding free energy remains largely unchanged. This behavior is analogous to condensation thermodynamics. In contrast, adding one (SA)₁(AM)₁ pair to form a (SA)₂(AM)₂ cluster results in a huge drop in the average free energy, as the addition causes a large stabilization at such small cluster sizes through a significant molecular rearrangement.

All thermochemistry during the sampling is performed under standard conditions with temperature 298.15 K and reference pressure 1 atm. Enthalpy ΔH and entropy ΔS are assumed to be constant on the given temperature scale for calculation of Gibbs free energies ΔG. As the default of ORCA, the quasi-harmonic approximation formulated by Grimme (2012) was applied to correct low (< 100 cm⁻¹) vibrational frequencies. All the calculated data are available in the Atmospheric Cluster Database (ACDB) (Elm, 2019).

2.1.3 Convex hull approach

We previously showed that, in the large SA–AM and SA–DMA cluster structures, fully coordinated ions emerged corresponding to a “solvated” ion with a “solvation” shell around it (Engsvang and Elm, 2022; Engsvang et al., 2023a; Wu et al., 2023). This can give a hint as to when we transition from clusters, where all monomers are exposed to the exterior, to a “solvated” structure more resembling the particle phase. However, obtaining such structural information from visual inspection of large clusters is difficult and prone to errors. To investigate when the first solvation shell appears in our cluster structures, here we employed the mathematical concept of a three-dimensional convex hull. A convex hull can be defined as the minimal convex set containing all the data. That is, it forms a polytope around the data with vertices as the “outermost” data points. Our approach is outlined as follows: the clusters are divided into monomers, and these monomers are then reduced to a single three-dimensional point at their center of mass (COM). Using the COM picture, we can compute the convex hull of the monomers, and we take this as the solvation shell. However, this can lead to situations where a monomer (COM) is located just inside the convex hull. That is, it will not be interpreted as part of the convex hull even though chemical intuition would not claim it to be a solvated monomer. To circumvent this issue, a rough estimate of the molecular radius is computed for all the monomers. This is done by simply computing the distance from the centroid of the monomer to all the atoms and averaging over the four largest of these distances. Then, if any COM is within a distance from a convex hull face that is less than its given molecular radius, it is included as the current solvation shell. After a solvation shell has been identified, the COMs included in this shell are removed from the dataset, and we iterate until all the data points are assigned to a solvation shell. The applied algorithm is freely available at https://gitlab.com/AndreasBuchgraitz/clusteranalysis (last access: 19 November 2024).

3 Results and discussion

3.1 Evaluation of the improvement workflow

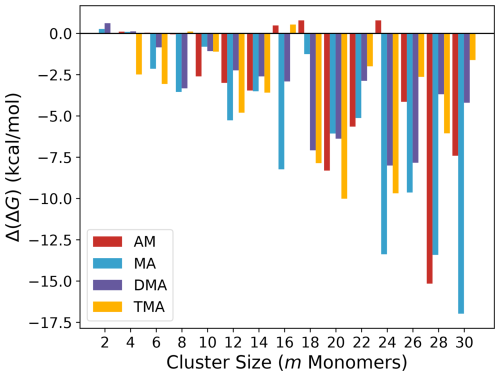
We initially evaluate how much of an improvement the addition of the CREST track is compared to only employing the ABC track. Figure 1 shows the difference in free energy at the B97-3c level of theory for the lowest configuration found by the original workflow given by the ABC track and the improvement workflow given by the CREST track for the (SA)_n(AM/MA/DMA/TMA)_n clusters, with n=1–15. We note that the monomer count (m) here is simply the number of molecules in the cluster (m=2n).

Figure 1 Difference in the free energy minimum found by the CREST track and the ABC track.

The addition of the CREST track significantly improves the free energy minimum found for almost all of the studied clusters. The improvements scale roughly with the system size, where for the smallest clusters (m=2–4) no improvements are seen and, in some cases, the located free energy minimum is slightly higher in free energy. This is caused by the potential energy surfaces of such small clusters being sampled well with ABCluster using rigid monomers, and there is nothing to be gained by including the extra dynamic CREST step. Already for m=6 the free energies after the CREST track are significantly lower. The largest improvement is seen to be a lowering of up to 17 kcal mol⁻¹ in the free energy for the (SA)₁₅(MA)₁₅ cluster. Figure 2 presents the two different (SA)₁₅(MA)₁₅ cluster structures, calculated at the B97-3c level of theory.

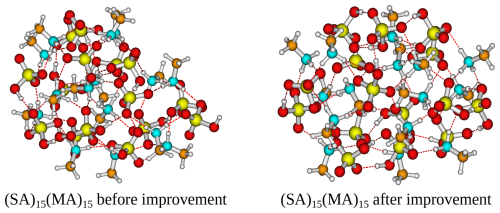
Figure 2 Structure of the (SA)₁₅(MA)₁₅ cluster that is lowest in free energy at the B97-3c level of theory before improvement (ABC track) and after improvement (CREST track).

It is seen that the (SA)₁₅(MA)₁₅ cluster after the CREST track is much more spherical compared to before. This leads to a more intricate hydrogen bond network and could explain the free energy difference. For most cluster sizes, the largest improvements are seen for the AM and MA clusters. The different hydrogen bond capacity of the base molecules most likely causes this effect. That is, the bulkier DMA and TMA molecules will have deeper minima as there needs to be a perfect match between the hydrogen bond donors and acceptors. This is in most cases captured relatively well by the ABCluster genetic algorithm. However, there are many more possible arrangements for AM and MA, which likely favours molecular dynamics sampling using CREST.

3.2 Cluster structures – the convex hull approach

We are interested in identifying the cluster size at which we observe a solvated ion with a full solvation shell around it, as this could be an indication of the cluster-to-particle transition point. It should be noted that such a solvation was previously observed by Ling et al. (2017) in NA–AM clusters (NA is nitric acid); by DePalma et al. (2012), Engsvang and Elm (2022) and Engsvang et al. (2023a) in SA–AM clusters; and by DePalma et al. (2014) and Wu et al. (2023) in SA–DMA clusters. Here, we elaborate on this concept further and connect it to the chemical composition of the clusters.

Figure 3 presents the number of solvation shells identified with the three-dimensional convex hull algorithm, described in Sect. 2.1.3 as a function of the cluster size (number of monomers m). We used the lowest free energy clusters for each of the four systems (SA)_n(AM)_n, (SA)_n(MA)_n, (SA)_n(DMA)_n and (SA)_n(TMA)_n for n=2–15 (m=2n).

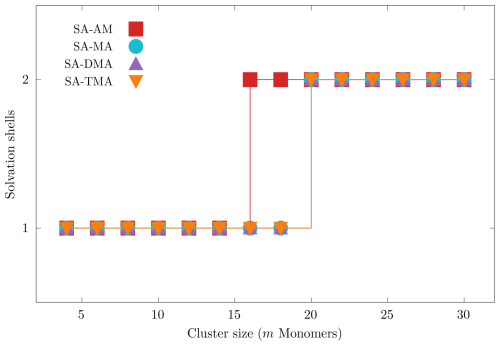
Figure 3 Number of identified solvation shells found using the convex hull approach for the lowest free energy (SA)_n(AM)_n, (SA)_n(MA)_n, (SA)_n(DMA)_n and (SA)_n(TMA)_n systems, with $n=\mathrm{2}-\mathrm{15}$ (m=2n).

We see that for all our cluster systems we identify a maximum of two solvation shells at the largest sizes (m=30). We find that solvation happens at m=16 for the SA–AM system and at m=20 for the SA–MA, SA–DMA and SA–TMA systems. We find that either the bases or a bisulfate can be found in the core of the cluster depending on the cluster composition and size. In the future it would be interesting to study the emergence of the first solvation shell using semiempirical molecular dynamics simulations.

3.3 Binding free energies

Figure 4 shows the calculated binding free energies of the (SA)_n(AM/MA/DMA/TMA)_n clusters, with n=1–15. The free energies are calculated at the B97-3c level of theory at 298.15 K and 1 atm. Panel (a) shows the total binding free energies, panel (b) shows the binding free energies per monomer m, and panel (c) shows the addition free energy of an acid–base pair.

As also seen in previous studies (DePalma et al., 2012, 2014; Engsvang and Elm, 2022; Engsvang et al., 2023a), the binding free energy more or less linearly decreases as a function of the cluster size m (see Fig. 4a). At m≥10, the order in the total binding free energies follows, TMA < AM < DMA < MA, and no longer changes as the cluster size increases. This is an interesting trend, as SA–base cluster formation is usually connected with the gas-phase basicity of the base for small clusters. However, for larger clusters, this appears not to be the case. This effect was already alluded to in the work of Temelso et al. (2018).

It should be noted that the linearly decreasing trend is dependent on the cluster composition and requires strongly binding clusters. For instance, in the previous work done by Myllys et al. (2021) (as shown in Figs. 1, 6 and 10 of their paper), the ΔG_bind of (SA)₁(base)₁(H₂O)_n is plotted against the number of water molecules n (where $n=m-\mathrm{2}$, with m being the total monomer count, including one SA molecule and one base molecule). In all these cases the free energy is not simply linearly decreasing, as the intermolecular interactions are quite weak. For instance, hydration of bases even gives an increasing free energy as a function of water molecules (see Myllys et al., 2021, Fig. 1).

At the initial clustering (with m=2), the binding strength follows the order AM < MA < TMA < DMA. This matches observations from experiments by Jen et al. (2014) on the base stabilization of sulfuric acid dimers. The order is also relatively consistent with prior theoretical work (Kurtén et al., 2008; Olenius et al., 2017; Temelso et al., 2018; Elm, 2021a; Kubečka et al., 2023b), except for the change in the order of DMA and TMA. Table 1 presents the calculated literature values for the binding free energies of the (SA)₁(base)₁ clusters compared to the current work.

Table 1 Comparison between different calculated values (kcal mol⁻¹) of the binding free energies of the (SA)₁(base)₁ clusters, with bases AM, MA, DMA and TMA. All values are calculated at 298.15 K and 1 atm.

^a Kurtén et al. (2008): RI-CC2/aug-cc-pV(T+)Z//RI-MP2/aug-cc-pVDZ, harmonic.
^b Temelso et al. (2018): MP2-F12/cc-pVTZ-F12//MP2/aug-cc-pVDZ, harmonic.
^c Olenius et al. (2013, 2017): RI-CC2/aug-cc-pV(T+)Z//B3LYP/CBSB7, harmonic.
^d Elm (2021a): DLPNO-CCSD(T₀)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p), quasi-harmonic.
^e This work: B97-3c, quasi-harmonic.
^f This work: DLPNO-CCSD(T₀)/aug-cc-pVTZ//B97-3c, quasi-harmonic.

In most previous quantum chemistry studies, the (SA)₁(DMA)₁ and (SA)₁(TMA)₁ clusters have very similar binding free energies. The values calculated at the RI-CC2/aug-cc-pV(T+)Z//B3LYP/CBSB7 level most likely yield overly negative binding free energies (Schmitz and Elm, 2020), and the DLPNO-CCSD(T₀)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level most likely underestimates the binding free energies (Myllys et al., 2016). The true value is most likely in between these two extremes. The B97-3c calculated free energies in this work agree relatively well with the literature values and should produce the correct trends. However, the values are greatly improved by refining the single point energy with a high-level DLPNO-CCSD(T₀)/aug-cc-pVTZ calculation. Unfortunately, such calculations are too expensive to apply to the full set of (SA)_n(base)_n clusters, with n up to 15. However, this indicates that higher-level single point energies should be calculated on top of the B97-3c structures to improve the values in the future. This is consistent with the conclusion of Engsvang et al. (2023a) for large SA–AM clusters.

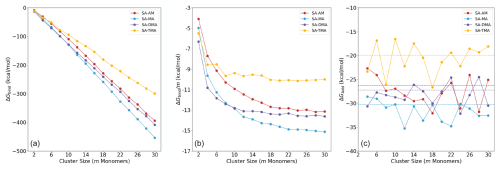
Figure 4 (a) Total binding free energies of (SA)_n(AM/MA/DMA/TMA)_n clusters, n=1–15. (b) Size-averaged binding free energy contribution in the clusters. (c) Acid–base pair addition free energies ΔG_add of the four SA–base clusters. (The dotted line indicates the values of $\mathrm{2}\times \mathrm{\Delta }{G}_{\mathrm{bind}}/m$ with m=30, and the values were multiplied by 2 as we present pair addition here.) The data of SA-AM/DMA are from our prior work (Wu et al., 2023), with additional sampling carried out in this work.

In Fig. 4b, it can be seen that, at m≥20, the curve of $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ levels out and the gradient of the size-averaged binding free energy $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ approaches zero. At this point the binding strength order of TMA < AM < DMA < MA also stays consistent. The SA–MA system exhibits the highest stability, with the most negative binding free energy across the m≥10 range converging at a value of −14.9 kcal mol⁻¹ at m=30. This is closely followed by the SA–DMA system, which converges at a value of −13.4 kcal mol⁻¹ at m=30. The SA–AM system is slightly less stable (−13.1 kcal mol⁻¹ at m=30), while the SA–TMA system has the highest binding free energy, indicating that it is the least stable of the four modeled systems (−10.1 kcal mol⁻¹ at m=30). Also, within m≤8 the stability of the SA–TMA system is highly dependent on the total number of SA–TMA pairs. For m=4, our calculations show that (SA)₂(TMA)₂ is less stable than (SA)₂(DMA)₂, which is in agreement with Elm (2021a) and Kubečka et al. (2023b). The low stability of the SA–TMA clusters at large sizes can be understood by the high steric hindrance introduced by the three methyl groups in TMA. In a similar fashion, the change in the order of MA, becoming more stable than DMA at m=10, can be attributed to a combination of binding strength, hydrogen bond capacity and steric hindrance.

As shown in Fig. 4c, the acid–base pair addition free energies ΔG_add fluctuate around the convergence value of the size-averaged binding free energy per monomer, $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ (indicated by the dotted lines). Since the addition free energy ΔG_add is the accurate quantity for estimating cluster stability, the relation between addition free energy ΔG_add and size-averaged binding free energy $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ is significant. Mathematically, taking the endpoint at m of the size-averaged binding free energy $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ corresponds to calculating the average of the addition free energies up to cluster size m. This approach helps determine the cluster size m at which fluctuations in ΔG_bind become negligible relative to the entire system. Furthermore, the convergence value of $\mathrm{\Delta }{G}_{\mathrm{bind}}/m$ can be used to estimate the free energies of acid–base pair additions to large clusters.

At large m, the low gradient of size-averaged binding free energies implies that at this point the average addition of monomers to the cluster does not change the uptake properties. We interpret this as the cluster showing particle-like properties. This also illustrates that when studying large clusters in the future we will not need to go beyond 20 monomers as the properties are already well converged at this point. On the other hand, there is a large stabilization achieved by adding more acid–base pairs for m≤ 8. Hence, we can divide the cluster formation process into two different regimes: an initial “cluster stabilization” regime for m≤ 8 and an FNP regime at m≥20. The cluster stabilization regime is highly dependent on the identity of the base molecule and governs the initial particle formation rate, while the freshly nucleated particle regime governs the particle growth. We will denote the transition between these two regimes as the cluster-to-particle transition regime. The observed leveling out in the average free energies also coincides with the emergence of the second solvation shell observed in Sect. 3.2. Hence, we suggest defining the cluster-to-particle transition point around m=16–20 and will denote clusters that have passed this point as FNPs. We note that the cluster-to-particle transition point presented here is conceptually new and fundamentally different from the concept of a “critical cluster” in classical nucleation theory, which resembles a maximum on the free energy surface. It should be mentioned that the onset of FNPs is highly dependent on the cluster composition, temperature and concentration of the clustering monomers. It should be noted further that we only study the FNPs in increments of acid–base pairs in the current work and that the cluster-to-particle transition point might change once data on monomer additions and evaporation become available.

3.4 Free energies under given conditions

Using the free energies calculated above, it is possible to calculate the binding free energies under specific conditions of monomer concentrations and temperature. This indicates whether these FNPs will actually be formed under realistic atmospheric conditions. The self-consistent distribution function proposed by Wilemski and Wyslouzil (1995) was employed to establish the monomer free energies as zero. Under the given conditions, the “actual” binding free energies were calculated by Halonen (2022): $\mathrm{\Delta }{G}_{\mathrm{bind}}\left(\mathit{p}\right)=\mathrm{\Delta }{G}_{\mathrm{bind}}^{\circ }+\mathrm{RT}(\mathrm{1}-\frac{\mathrm{1}}{n}){\sum }_i\ln \left(\frac{p_i}{p_{\mathrm{ref}}}\right)$, where p_ref corresponds to a reference pressure (1 atm) and p_i represents precursor (in our discussion, monomer) partial pressures. This equation differs from previous work on cluster formation under actual conditions as these incorrectly generalized the unimolecular nucleation equation. Thus, the equation also satisfies self-consistency for multicomponent systems, i.e., with zero free energies for all precursors. We tested the different formulations of the actual free energies under the given conditions and found no deviations between the calculated free energies in the current work.

Figure 5 shows the actual binding free energies ΔG_bind of the (SA)_n(AM/MA/DMA/TMA)_n clusters (n = 1–15) under given conditions. The figures are plotted as a function of the number of monomers (m) in the clusters (m=2n). We studied two temperatures of 298.15 and 278.15 K given by the red and blue shadings, respectively. The concentration of SA was fixed at [SA] = 10⁶ molec. cm⁻¹. We studied two different concentrations of the bases: a “High Conc.” limit with [AM] = 10 ppb and [MA] = [DMA] = [TMA] = 10 ppt as well as a “Low Conc.” limit with [AM] = 10 ppt and [MA] = [DMA] = [TMA] = 1 ppt. We note that the chosen values of the amines should be viewed as an upper limit in non-polluted environments. Similarly, the concentration of SA could also easily exceed 10⁶ molec. cm⁻¹ in many environments.

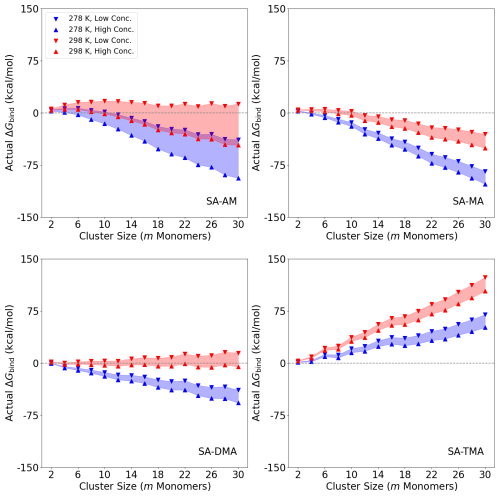
Figure 5 Binding free energies ΔG_bind of the (SA)_n(AM/MA/DMA/TMA)_n clusters (n = 1–15, m=2n) under given temperature and concentration conditions. High temperature (298.15 K) is where the concentration range is filled with red shading and accordingly low temperature (278.15 K) with blue shading. [SA] was fixed at 10⁶ molec. cm⁻¹. “High Conc.” refers to high concentration, with [AM] = 10 ppb and [MA] = [DMA] = [TMA] = 10 ppt (upward-pointing triangle). “Low Conc.” refers to low concentration, with [AM] = 10 ppt and [MA] = [DMA] = [TMA] = 1 ppt (downward-pointing triangle).

It is seen that temperature plays a more important role than the monomer concentrations for all the systems. Increasing the concentration of the base by 1 order of magnitude, the free energy decreases by ∼2.5 kcal mol⁻¹ per monomer. When decreasing the temperature from 298.15 to 278.15 K, the free energy decreases by ∼6 kcal mol⁻¹ per monomer. For SA–AM there is a nucleation barrier at both temperatures, which should limit the cluster formation process under such conditions. This is consistent with the previous work by Olenius et al. (2013) and Besel et al. (2019), which showed that ions are important for boosting SA–AM nucleation. It should be mentioned that the actual nucleation barrier of the system cannot be determined based solely on the 1:1 acid–base ratio composition. Monomer condensation could potentially lead to a change in the barrier. However, in most SA–base systems the 1:1 ratio is the most stable composition (Olenius et al., 2013; Elm et al., 2017a), and if the 1:1 ratio does indeed show a barrier, then the ± 1 acid / base molecule systems will have to cross that as well.

The SA–AM system is highly dependent on concentration, which is caused by a larger concentration range (10 ppt–10 ppb) compared to MA, DMA and TMA (1–10 ppt). The SA–MA system also has a nucleation barrier at 298.15 K and a low concentration (1 ppt) but no barrier under the other studied conditions. The SA–DMA cluster system is seen to form without a nucleation barrier at a low temperature (278.15 K). This finding is consistent with the previous work by Olenius et al. (2013) and the experiments at CLOUD, which showed that SA–DMA cluster formation occurs at the kinetic limit at temperatures of 278.15 K or below (Kürten et al., 2014, 2018).

Interestingly, in all cases of m≥6, the SA–TMA clusters are very unstable and hardly bind with SA under any of the studied conditions. This indicates that TMA is only important in the cluster stabilization regime and does not help grow the particles at larger sizes under these conditions. This finding is consistent with previous quantum chemical studies (Kubečka et al., 2023b) and observations (Cai et al., 2023). This makes sense from a molecular perspective, as TMA, after proton transfer from SA, only has one hydrogen bond donor, and the three bulky methyl groups will lead to high steric hindrance. Hence, the hydrogen bond capacity of the base is quite important for the cluster growth. However, this contradicts the experimental results of Glasoe et al. (2015), where 1.8 nm sulfuric acid–base particle formation followed an AM < MA < DMA < TMA trend. As Glasoe et al. (2015) used a quite high concentration of sulfuric acid ([SA] = 10⁹–10¹⁰ molec. cm⁻¹), one reason for this discrepancy could be our fixed 1:1 ratio of sulfuric acid to bases. Hence, in the future, it might be worth investigating large clusters where the SA–base ratio is higher, instead of the usual 1:1 ratio.

The fact that the bases behave very differently as a function of the number of monomers in the cluster could indicate that SA–mixed-base systems are worth studying in the future. For instance, it is very likely that strong bases such as DMA and TMA are primarily important in the very initial steps and that the subsequent growth is entirely driven by the weaker bases AM and MA. This was previously hypothesized for smaller clusters (Elm, 2017; Elm et al., 2017b; Elm, 2021b) but not definitively proven. Hence, large SA–AM–DMA or SA–MA–DMA clusters up to the cluster-to-particle transition point will be worth studying in the future. This will also allow us to study base substitution in such systems and investigate whether ammonia is efficiently substituted by DMA, as illustrated by Kupiainen et al. (2012) for smaller clusters.

3.5 Cluster populations

A common assumption when studying atmospheric molecular clusters is to only use the lowest free energy configuration to describe the cluster properties. Hence, it is assumed that the lowest free energy configuration is dominantly populated and that the global minimum is reached rapidly via molecular rearrangement. However, whether this is valid for larger clusters remains unknown. To investigate this aspect, we calculated the populations of the four lowest free energy configurations for the studied SA–base systems. Different cluster configurations were determined via RMSD as described in Sect. 2.1.1. As a method to tell conformational differences, RMSD is less intuitive than measures such as internal coordinates (bond lengths, angles, etc.) when applied to small molecules or clusters. For large systems such as proteins, supramolecules or large clusters, all-atom RMSD is computationally expensive and has the risk of the geometrical information of interest being averaged out by the large number of atoms, leading to a low signal-to-noise ratio. In our cases of studying large clusters, the detailed difference of the monomer side group (e.g., rotation of methyl or hydroxy groups) should not, aside from minor inductive effects, affect the intermolecular interactions significantly. Similarly, in protein science, a widely used simplification is to use α-C atoms to represent amino acids, and RMSD or other distance-based metrics are then calculated based only on the positions of the α-C atoms (Lazar et al., 2020). Hence, during the comparison, we compared the geometries containing only sulfur and nitrogen atoms. Thereby, in this comparison, the RMSD contributions to the differences between monomer side chains are neglected.

Figure 6 shows the configurational population of the (SA)_n(base)_n systems with n=1–15, plotted as a function of the monomer count (m=2n). Only the four lowest free energy configurations were plotted: they were calculated at 298.15 K and 1 atm. This is also the reason for the populations not summing up to 100 % in all the cases.

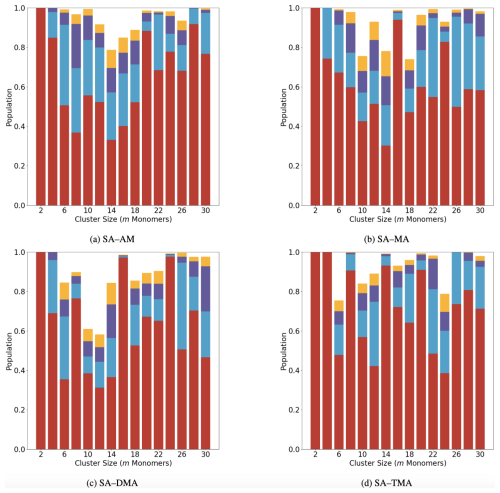
Figure 6 Population distribution of the lowest four configurations of the (SA)_n(AM/MA/DMA/TMA)_n clusters (n = 1–15, m=2n).

Figure 6 shows that the lowest configuration is fully populated at m=2. In general, a decreasing trend of the population weight of the lowest free energy configuration is seen from m=4 to 14, indicating that, as the cluster size grows, more configurations will co-exist. At sizes larger than m=14, the population of the lowest configuration begins to increase again. This is counterintuitive and is likely an artifact of the averaging nature of the RMSD calculation. Calculating RMSD with only S and N atoms removes the contribution from the methyl group rotation or the bending of the S–O–H angle. However, for large clusters such as those studied here, the geometric difference contributed by a certain local substructure in the cluster is lost when averaging over the total number of atoms. We note that, in order to properly identify unique configurations, methods other than the conventional RMSD should be tested. In the future we will test other methods for isolating the different configurations, such as mass-weighted RMSD and contact maps.

The binding free energies of the four lowest configurations are listed in the supporting information (see Table S3 and S4 in the Supplement). The energy gap between the lowest and second lowest configurations is in most cases below 1 kcal mol⁻¹ (the largest value of 2.9 kcal mol⁻¹ appears for (SA)₈(DMA)₈). It should be noted that the configuration above 3 kcal mol⁻¹ from the lowest free energy minimum will have a negligible contribution to the multi-configurational free energy at 298 K (Partanen et al., 2016). Nevertheless, in all the cases we can see a large weight (≥30%) on the lowest free energy cluster structure. Furthermore, by comparing the binding free energies of the lowest-energy configurations in Table S1 in the Supplement with the multi-conformer binding free energies in Table S2, it is evident that including all the identified configurations (filtered by RMSD with a threshold of 0.4 Å) reduces the effective binding free energies by less than 1 kcal mol⁻¹. This indicates that, when looking at the properties of these large cluster systems, one can safely study the one to two clusters lowest in free energy without introducing large uncertainties. Hence, in the future we can study how the FNPs take up vapor molecules, how evaporation occurs from them, and how chemical reactions occur at the surface by using the lowest clusters found here.

4 Conclusions

In this work we presented quantum chemical modeling of large (SA)_n(AM/MA/DMA/TMA)_n clusters, with n = 1–15 (cluster size m = 2–30), at the B97-3c level of theory. A comprehensive configurational sampling protocol was applied to locate the lowest free energy cluster structures. When there are around 16–20 monomers (m) in the cluster, we see the emergence of the first solvation shell, where an ion is fully coordinated inside the cluster core. The binding free energies (at 298.15 K and 1 atm) per monomer in the cluster showed that the cluster growth process can be divided into a cluster stabilization regime for m≤8 and a freshly nucleated particle (FNP) regime at m≥20, where the structure and stability of the molecular cluster more resemble particle-like properties. Consistent with previous studies, we find that the cluster stabilization regime is highly dependent on the clustering base molecule. Based on these findings, we define the cluster-to-particle transition point as the onset of FNPs to be around 16–20 monomers.

Studying the free energies under given conditions, we find that the SA–AM and SA–MA systems have a nucleation barrier, SA–DMA forms clusters below 278.15 K without a barrier, and SA–TMA does not form stable clusters at m≥6 monomers. This contradicts experimental results on 1.8 nm particles and could indicate that the 1:1 ratio of acids to bases is not the most likely growth pathway for all of the larger clusters. Hence, under realistic experimental conditions, the presence of water and other species might enable the growth of SA–TMA clusters.

We studied the cluster populations and found that a great weight is placed on the lowest free energy cluster structure. This indicates that the lowest free energy cluster configurations can be used to study the properties of these clusters in the future.

The fact that the different bases appear to be very important in the different regimes could indicate that large SA–mixed-base clusters should be studied in the future to disentangle which bases are important for nucleation and which are important for growth. In addition, the growth of the clusters should be investigated further, i.e., calculating clusters that differ from the 1:1 acid–base ratio. This will also enable the possibility of performing cluster dynamics simulations. Finally, the inclusion of water should also be investigated, as it might have a large influence on the cluster stabilities and by extension the cluster-to-particle transition point.