Charging, aggregation, and electrostatic dispersion of radioactive and nonradioactive particles in the atmosphere

Electrostatic dispersion can significantly impact the microphysical behavior of charged particles and ions until reaching zero space charge. However, although radioactive particles can be strongly charged in air, the influence of electrostatic dispersion has been neglected in understanding their behavior. This study is aimed at investigating the time evolution of the charge and size distributions of radioactive and nonradioactive particles in air and developing simple approaches for applications. With processes involving charging, aggregation, and electrostatic dispersion, a comprehensive population balance model (PBM) has been developed to examine particle charge/size distribution dynamics. It is shown that compared to nonradioactive particles, the charge and size distributions of radioactive particles may evolve differently with time because radioactivity and electrostatic dispersion can significantly affect the charging and aggregation kinetics of the particles. It is found that, after the Fukushima accident, background aerosols in the pathway of radioactive plumes might be highly charged due to ionizing radiation, suggesting that radiation fields may strongly influence in situ measurements of charged atmospheric particles. The comprehensive PBM is simplified, and then the verification and application of the simplified PBMs are discussed. This study provides useful insight into how radioactivity can affect the dynamic behavior of particles in atmospheric systems including radiation sources.

1 Introduction

Charge and size, the dynamically evolving properties of particles, can govern microphysical processes in various atmospheric systems such as ambient air (Tripathi and Harrison, 2001), containment systems of nuclear reactors (Clement et al., 1995), dusty plasma (Fortov et al., 2001), human respiratory systems (Cohen et al., 1998), particle measurement systems (Rosinski et al., 1962; Yeh et al., 1978; Gensdarmes et al., 2001), radioactive neutralizers (Cooper and Reist, 1973), and thermal spas (Nikolopoulos and Vogiannis, 2007). In these systems, the charge and size of particles can affect their charging, aggregation, and dry and wet depositions, which are also vital processes in radioactivity transport modeling (Hu et al., 2014; Katata et al., 2012; Kim et al., 2014, 2015, 2016) and in situ measurements of charged particles (Renard et al., 2013). These systems can include various radiation sources such as natural radioactivity (Nikolopoulos and Vogiannis, 2007) and fission products (Clement et al., 1995; Cooper and Reist, 1973; Fortov et al., 2001; Gensdarmes et al., 2001; Rosinski et al., 1962; Tripathi and Harrison, 2001; Yeh et al., 1978). Because such radiation sources can affect the particle charge and size distributions, understanding the influence of radioactivity is necessary to investigate microphysical processes in atmospheric systems containing radionuclides.

Radioactivity is a property of atoms emitting energetic particles such as alpha and beta particles (Sawyer et al., 1994). The release of energetic particles can lead to charge accumulation on radioactive and nonradioactive particles due to self-charging and diffusion charging mechanisms (Clement and Harrison, 1992; Kim et al., 2014; Kweon et al., 2013; Walker et al., 2010; Yeh et al., 1978). The charging of particles may subsequently affect their size growth by aggregation (Clement et al., 1995; Kim et al., 2016), the removal of the particles by rain scavenging (Tripathi and Harrison, 2001), and adsorption/condensation of gas molecules on the particles (Kweon et al., 2015) by generating electrostatic interactions. However, radioactivity-induced charging and the subsequent charging effects have been typically neglected in modeling studies of radioactivity transport, mainly due to insufficient information on particle charge/size distribution dynamics (Hu et al., 2014) and lack of simulation tools to couple particle transport with charging effects.

Previous attempts to incorporate electrostatic interactions into charge/size distribution dynamics include the work of Clement and Harrison (1992) and Clement et al. (1995), who investigated radioactivity-induced charging and its subsequent influence on particle collision. However, these investigations assumed no size evolution of radioactive particles. Adachi et al. (1981), Oron and Seinfeld (1989a), and Vemury et al. (1997) developed sectional models to predict time-dependent changes in the charge and size distributions of particles undergoing aggregation and electrostatic dispersion, but the models excluded particle–ion dynamics. Oron and Seinfeld (1989b) improved the sectional model to include particle–ion dynamics, but the model is still not applicable to radioactive particles because self-charging was omitted. Thus, a more comprehensive predictive model is required to examine charge/size distribution dynamics of radioactive and nonradioactive particles in the atmosphere.

This study is focused on investigating the time evolution of charge and size distributions of radioactive and nonradioactive particles using a bivariate population balance model (PBM), which includes charge and size as independent variables. In our previous work (Kim et al., 2015, 2016), particle–ion dynamics and radioactivity-induced charging were coupled to develop a bivariate PBM. In the present study, we have incorporated electrostatic dispersion of particles and ions into the bivariate PBM to more comprehensively consider electrostatic interactions. The bivariate PBM has been simplified by reducing the number of the independent variables. The verification and application of the simplified PBM have been discussed.

2 Background: electrostatic interactions of charged objects

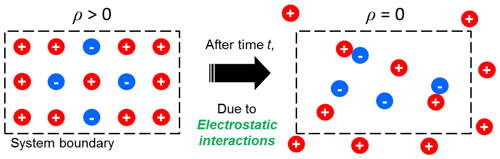
Interactions of electrical charge result in the production of electrostatic forces between charged objects such as colloidal particles and ions (Chin et al., 1998; Tsouris et al., 1995; Taboada-Serrano et al., 2005). In a spatially homogeneous atmospheric system containing charged particles and ions, positively charged particles can easily collide with negatively charged particles and negative ions because of electrostatic attractive forces generated between positive and negative charges. Concurrently, the positively charged particles mutually repel each other and positive ions because of electrostatic repulsive forces. In particular, as shown in Fig. 1, mutual repulsion may lead to the transport of positively charged particles and positive ions outside the system boundaries until the system reaches charge equilibrium, as follows:

$$\begin{array}{}\text{(1)}& \mathit{\rho }=e\left[n_{+}-n_{-}+\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}j\sum _{k=\mathrm{1}}^M{N}_{k,j}\right]=\mathrm{0},\end{array}$$

where ρ is the space charge density, e is the electrical charge, n_± represents the concentrations of positive and negative ions, j is the number of elementary charge carried by individual particles, and M is the total number of size bins.

Figure 1 Electrostatic interactions of charged objects in a spatially homogeneous colloidal system.

As shown in Fig. 1, the transport of charged particles and ions by electrostatic repulsion can decrease their concentrations in the system (Oron and Seinfeld, 1989a, b):

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}{N}_{k,j}}{\mathrm{d}t}}=-{\displaystyle \frac{B_{k}je{N}_{k,j}\mathit{\rho }}{\mathit{\epsilon }}},\text{(3)}& {\displaystyle \frac{\mathrm{d}{n}_{\pm }}{\mathrm{d}t}}=\mp {\displaystyle \frac{{\mathit{\mu }}_{\pm }{n}_{\pm }\mathit{\rho }}{\mathit{\epsilon }}},\end{array}$$

where N_k,j is the concentration of size k particles carrying elementary charge j, B is the particle mobility, μ_± are the mobilities of positive and negative ions, and ε is the permittivity of vacuum. This phenomenon has been observed in many laboratory-scale experiments and has been called electrostatic dispersion (Whitby et al., 1965; Adachi et al., 1981; Kasper, 1981). Additional processes that can decrease the ion and particle concentration include recombination, attachment, aggregation, and deposition.

3 Model development

3.1 Bivariate population balance model (PBM)

In a spatially homogeneous system, the size and charge distributions of radioactive and nonradioactive particles can be simultaneously influenced by charging, aggregation, and electrostatic dispersion. Time evolution of the distributions by the first two processes can be predicted using a bivariate PBM with two independent variables, namely size and charge (Kim et al., 2015, 2016). The effects of electrostatic dispersion on the distributions can be taken into account by incorporating Eq. (2) into the bivariate PBM as follows:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{N}_{k,j}}{\mathrm{d}t}}& =s{A}_k\left(N_{k,j-s}-N_{k,j}\right)+{\mathit{\beta }}_{k,j-\mathrm{1}}^{+}{n}_{+}{N}_{k,j-\mathrm{1}}\\ & -{\mathit{\beta }}_{k,j}^{+}{n}_{+}{N}_{k,j}+{\mathit{\beta }}_{k,j+\mathrm{1}}^{-}{n}_{-}{N}_{k,j+\mathrm{1}}-{\mathit{\beta }}_{k,j}^{-}{n}_{-}{N}_{k,j}\\ & +\sum _{j^{\prime }=-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{\begin{array}{c}l,m\\ x_{k-\mathrm{1}}\le x_l+x_m\le x_{k+\mathrm{1}}\end{array}}^{l\ge m}\\ & \left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\delta }}_{l,m}^{\mathrm{Kr}}\right){\mathit{\eta }}_{l,m}{F}_{l,m,j-j^{\prime },j^{\prime }}{N}_{l,j-j^{\prime }}{N}_{m,j^{\prime }}\\ & -\sum _{j^{\prime }=-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{l=\mathrm{1}}^M{F}_{k,l,j,j^{\prime }}{N}_{k,j}{N}_{l,j^{\prime }}-{\displaystyle \frac{B_{k}je{N}_{k,j}\mathit{\rho }}{\mathit{\epsilon }}},\end{array}\end{array}$$

where s is the self-charging coefficient (i.e., the number of charges accumulated on single particles per decay), A_k is the radioactivity of single particles, ${\mathit{\beta }}_{k,j}^{\pm }$ represents the ion–particle attachment coefficients, l and m are the size bin numbers, δ^Kr is the Kronecker delta, η is a property distribution factor between two size bins, and F is the aggregation frequency.

The first term on the right-hand side (RHS) of Eq. (4) accounts for the self-charging of radioactive particles. The second to fifth terms represent diffusion charging resulting from diffusion of positive and negative ions onto particles. The sixth and seventh terms account for the production and loss of particles via aggregation. The last term represents the loss of particles by electrostatic dispersion.

In Eq. (4), particle charging is parameterized by s, A_k, ${\mathit{\beta }}_{k,j}^{\pm }$, and n_±. The self-charging coefficient, s, is characteristic of the decay modes of radionuclides (e.g., s = 9 for ²³⁸PuO₂ (Yeh et al., 1978); s = 1 for beta-emitting particles (Clement and Harrison, 1992)). For a homogeneous radioactive particle population, the activity of single radioactive particles increases as the particle size increases because large particles contain more radionuclides. The activity of size k particles was estimated according to Clement et al. (1995) and Kim et al. (2017). Note that for nonradioactive particles, the self-charging term disappears from Eq. (4) because the particle radioactivity is zero (i.e., A_k = 0). The ion–particle attachment coefficient, ${\mathit{\beta }}_{k,j}^{\pm }$, is highly influenced by the properties of particles and ions (e.g., particle size and ion mobility). Various sources and sinks affect the ion concentrations in the atmosphere; thus, n_± is given by an ion balance involving Eq. (3) (Oron and Seinfeld, 1989b; Kim et al., 2015, 2016):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{n}_{+}}{\mathrm{d}t}}=-n_{+}\sum _k\sum _j{\mathit{\beta }}_{k,j}^{+}{N}_{k,j}-{\mathit{\alpha }}_{\mathrm{rc}}{n}_{+}{n}_{-}-{\displaystyle \frac{{\mathit{\mu }}_{+}{n}_{+}\mathit{\rho }}{\mathit{\epsilon }}}+q,\text{(6)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{n}_{-}}{\mathrm{d}t}}& =-n_{-}\sum _k\sum _j{\mathit{\beta }}_{k,j}^{-}{N}_{k,j}-{\mathit{\alpha }}_{\mathrm{rc}}{n}_{+}{n}_{-}\\ & +{\displaystyle \frac{{\mathit{\mu }}_{-}{n}_{-}\mathit{\rho }}{\mathit{\epsilon }}}+q+q_{\mathrm{e}},\end{array}\end{array}$$

where α_rc is the recombination rate coefficient of positive and negative ions, q is the production rate of ion pairs, and q_e is the generation rate of electrons. The first three terms on the RHS of Eqs. (5) and (6) represent the loss of ions by ion–particle attachment, ion–ion recombination, and electrostatic dispersion, respectively. Note that in Eq. (6), the sign of the third term is positive because negative ions can be removed by electrostatic dispersion when ρ < 0. The fourth term on the RHS of Eqs. (5) and (6) stands for ionization of air molecules by ionizing radiation. The last term on the RHS of Eq. (6) accounts for electrons emitted by radioactive decay.

For Brownian aggregation, the aggregation frequency in Eq. (4) can be estimated from the collision frequency, β^Br (Fuchs, 1989), as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\mathit{\beta }}_{\mathrm{kl}}^{\mathrm{Br}}& =\mathrm{2}\mathit{\pi }\left(d_k+d_l\right)\left(D_k+D_l\right)\\ & {\left({\displaystyle \frac{d_k+d_l}{d_k+d_l+\sqrt{{\mathit{\delta }}_k^{\mathrm{2}}+{\mathit{\delta }}_l^{\mathrm{2}}}}}+{\displaystyle \frac{\mathrm{8}\left(D_k+D_l\right)}{\left(d_k+d_l\right)\sqrt{{\stackrel{\mathrm{‾}}{v}}_k^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{v}}_l^{\mathrm{2}}}}}\right)}^{-\mathrm{1}},\end{array}\end{array}$$

with

$$\begin{array}{rl}& {\mathit{\delta }}_k={\displaystyle \frac{\mathrm{1}}{\mathrm{3}{d}_k{L}_k}}\left({\left(d_k+L_k\right)}^{\mathrm{3}}-{\left(d_k^{\mathrm{2}}+L_k^{\mathrm{2}}\right)}^{\frac{\mathrm{3}}{\mathrm{2}}}\right)-d_k,\\ & L_k={\displaystyle \frac{\mathrm{8}{D}_k}{\mathrm{3}{d}_k{\stackrel{\mathrm{‾}}{v}}_k}},{\stackrel{\mathrm{‾}}{v}}_k=\sqrt{{\displaystyle \frac{\mathrm{8}{k}_{\mathrm{B}}T}{\mathit{\pi }{x}_k}}},\end{array}$$

where d_k is the particle diameter, D_k is the diffusion coefficient of single particles, k_B is the Boltzmann coefficient, T is the temperature, and x_k is the mass of individual particles. Equation (7) does not include the effects of electrostatic particle–particle interactions on the aggregation frequency. The influence of electrostatic interactions can be included by multiplying the collision frequency, β^Br, by the collision efficiency, α^Br (Fuchs, 1989), as follows:

$$\begin{array}{}\text{(8)}& {\mathit{\alpha }}_{\mathrm{kl}}^{\mathrm{Br}}={\displaystyle \frac{z}{e^z-\mathrm{1}}},\end{array}$$

with z = $\frac{j_k{j}_l{e}^{\mathrm{2}}}{\mathrm{2}\mathit{\pi }\mathit{\epsilon }\left(d_k+d_l\right)k_{\mathrm{B}}T}$.

3.2 Simplification of bivariate PBM

For computational efficiency, the bivariate PBM can be simplified via two approaches (Adachi et al., 1981; Kim et al., 2016). The first approach focuses on tracking time evolution of the size distribution and mean charge of particles (Kim et al., 2016), while the second concentrates on predicting time-dependent changes in the charge distribution and mean size of particles (Adachi et al., 1981). Hereafter, we refer to the approaches by the monovariate and monodisperse PBMs, respectively.

3.2.1 Monovariate PBM

Changes in the particle charge and size distributions vs. time can be predicted using the simple charge balance and the monovariate PBM (Kim et al., 2016). Similar to the charging terms of Eq. (4), particle charging can be described using the four charging parameters: the self-charging coefficient, radioactivity per particle, ion–particle attachment coefficients, and ion concentrations (Clement and Harrison, 1992; Kim et al., 2014, 2016).

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}{J}_k}{\mathrm{d}t}}=s{A}_k+{\mathit{\beta }}_{k,J}^{+}{n}_{+}-{\mathit{\beta }}_{k,J}^{-}{n}_{-},\end{array}$$

where J_k is the mean charge of size k particles. The ion concentrations on the RHS of Eq. (9) can be obtained by simplifying the first terms on the RHS of Eqs. (5) and (6) as

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{d}{n}_{+}}{\mathrm{d}t}}=-n_{+}{\mathit{\beta }}_{k,J}^{+}{N}_k-{\mathit{\alpha }}_{\mathrm{rc}}{n}_{+}{n}_{-}-{\displaystyle \frac{{\mathit{\mu }}_{+}{n}_{+}\mathit{\rho }}{\mathit{\epsilon }}}+q,\text{(11)}& {\displaystyle \frac{\mathrm{d}{n}_{-}}{\mathrm{d}t}}=-n_{-}{\mathit{\beta }}_{k,J}^{-}{N}_k-{\mathit{\alpha }}_{\mathrm{rc}}{n}_{+}{n}_{-}+{\displaystyle \frac{{\mathit{\mu }}_{-}{n}_{-}\mathit{\rho }}{\mathit{\epsilon }}}+q+q_{\mathrm{e}}.\end{array}$$

The mean charge of size k particles predicted by solving Eqs. (9)–(11) can be approximately converted to the particle charge distribution using a Gaussian distribution:

$$\begin{array}{}\text{(12)}& N_{k,j}={\displaystyle \frac{N_k}{\sqrt{\mathrm{2}\mathit{\pi }}{\mathit{\sigma }}_k}}\exp \left(-{\displaystyle \frac{(j-J_k{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}_k^{\mathrm{2}}}}\right),\end{array}$$

where σ_k is the standard deviation given by Clement et al. (1995). The width and mean of the particle charge distribution can be influenced by the charging parameters. For example, in comparison to nano-sized aerosols, the charge distribution of micron-sized aerosols can be wider because they can capture more ions (e.g., see Wiedensohler, 1988, and Kim et al., 2017). Then, the approximate charge distribution is used to compute ρ and the rates of aggregation and electrostatic dispersion in the monovariate PBM with only the particle size as the independent variable, as follows:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{N}_k}{\mathrm{d}t}}& =\sum _{\begin{array}{c}l,m\\ x_{k-\mathrm{1}}\le x_l+x_m\le x_{k+\mathrm{1}}\end{array}}^{l\ge m}\\ & \left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\delta }}_{l,m}^{\mathrm{Kr}}\right){\mathit{\eta }}_{l,m}{F}_{l,m}{N}_l{N}_m\\ & -\sum _{l=\mathrm{1}}^M{F}_{k,l}{N}_k{N}_l-\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}{\displaystyle \frac{B_{k}je{N}_{k,j}\mathit{\rho }}{\mathit{\epsilon }}}.\end{array}\end{array}$$

In Eq. (13), the first two terms on the RHS account for particle aggregation. The third term describes electrostatic dispersion. The influence of distributed charges on particle aggregation can be involved by replacing Eq. (8) with the average collision efficiency (Kim et al., 2016):

$$\begin{array}{}\text{(14)}& {\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\mathrm{kl}}^{\mathrm{Br}}=\mathrm{1}+{\displaystyle \frac{{\sum }_{j_k{j}_l\ne \mathrm{0}}{N}_{k,j_k}{N}_{l,j_l}\left({\mathit{\alpha }}_{\mathrm{kl}}^{\mathrm{Br}}-\mathrm{1}\right)}{{\sum }_{j_k}{N}_{k,j_k}{\sum }_{j_l}{N}_{l,j_l}}}.\end{array}$$

3.2.2 Monodisperse PBM

Adachi et al. (1981) developed the monodisperse PBM to simulate aggregation and electrostatic dispersion of particles:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{N}_j}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{j^{\prime }=-\mathrm{\infty }}^{\mathrm{\infty }}F(V,j,j^{\prime })N_{j-j^{\prime }}{N}_{j^{\prime }}\\ & -\sum _{j^{\prime }=-\mathrm{\infty }}^{\mathrm{\infty }}F(V,j,j^{\prime })N_j{N}_{j^{\prime }}-{\displaystyle \frac{B\left(V\right)je{N}_j\mathit{\rho }}{\mathit{\epsilon }}},\end{array}\end{array}$$

where V is the average volume of particles. By assuming the monodisperse size distribution, the mean size of single particles can be given as follows (Vemury et al., 1997):

$$\begin{array}{}\text{(16)}& V={\displaystyle \frac{V_{\mathrm{t}}}{N_{\mathrm{t}}}},\end{array}$$

where V_t and N_t are the total volume and number concentration of particles, respectively. The charging terms of Eq. (4) can be easily modified and incorporated into Eq. (15) to include particle charging.

3.3 Algorithm to simulate electrostatic dispersion

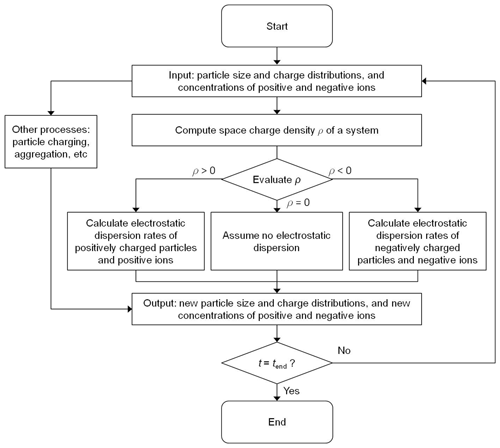
The aforementioned PBMs include the electrostatic dispersion terms. Figure 2 shows an algorithm to involve the effects of electrostatic dispersion on the time evolution of the particle charge and size distributions and ion concentrations. The algorithm allows the concentrations of particles and ions to decrease due to electrostatic dispersion when the space charge of the system is nonzero, as shown in Fig. 1. The electrostatic dispersion terms of the models disappear under a condition of zero space charge (e.g., the Boltzmann equilibrium).

Figure 2 Algorithm to simulate electrostatic dispersion of particles and ions.

3.4 Simulation

The PBM was used to investigate the dynamics of charge and size distributions of radioactive and nonradioactive particles. The models did not include parameters to consider the effects of electronegativity and affinity of the elements involved. For the investigation, we used MATLAB ode15s, which is typically employed to solve discrete population balance equations (e.g., see Jama et al., 2020). ²³⁸Pu, ¹³⁷Cs, and ¹³¹I were chosen as alpha- and beta-emitting radionuclides, respectively, because particles containing these radionuclides are typically studied in particle measurement systems, as well as model studies (Yeh et al., 1978; Clement and Harrison, 1992; Gensdarmes et al., 2001; Hu et al., 2014; Kim et al., 2015). The decay of ²³⁸Pu emits single-alpha particles with a kinetic energy of 5.593 MeV, while that of ¹³⁷Cs and ¹³¹I releases single-beta particles with mean kinetic energy of 0.1921 and 0.1812 MeV, respectively. To involve alpha and beta radiations leading to the ionization of air molecules during simulation, we assumed that ²³⁸Pu can produce 150 000 ion pairs per alpha decay, while ¹³⁷Cs and ¹³¹I can generate 2067 and 1945 ion pairs per beta decay, respectively. These values are the ionization rate coefficients of the radionuclides; the value for ²³⁸Pu was obtained from Clement and Harrison (1992), while the values for ¹³⁷Cs and ¹³¹I were given by Kim et al. (2015). Predictions using these values agreed well with charge measurements of the radioactive particles (Clement and Harrison, 1992; Kim et al., 2015). For diffusion charging, ${\mathit{\beta }}_{k,j}^{\pm }$ was computed from Fuchs (1963) and Hoppel and Frick (1986). For the computations because negative ions have typically higher mobility than positive ions, we assumed that μ₋ = 1.65 m² V⁻¹ s⁻¹, μ₊ = 1.15 m² V⁻¹ s⁻¹, m₋ = 80 atomic mass unit (amu), and m₊ = 150 amu (Alonso et al., 1997; Kim et al., 2016). Typical values for the properties of background air were quoted from Harrison and Carslaw (2003); (i) the air contains 5×10⁸ ion pairs per cubic meter, (ii) the background ionization rate is 10⁷ ion pairs per cubic meter per second, and (iii) α_rc is $\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{12}}$ m⁻³. These values may represent atmospheric conditions of the lower troposphere (Harrison and Carslaw, 2003; Stozhkov, 2003). For discretization, similarly to Oron and Seinfeld (1989a), we assumed a geometric grid (i.e., x_k+1 = 2x_k).

4 Results and discussion

4.1 Verification of bivariate PBM

The bivariate PBM includes four processes causing electrostatic interactions, namely self-charging, diffusion charging, aggregation, and electrostatic dispersion. The first three processes of the bivariate PBM were verified in our previous work (Kim et al., 2015, 2016). In brief, the bivariate PBM, excluding electrostatic dispersion, accurately predicted the charging and aggregation of radioactive and nonradioactive particles under various initial conditions. In the present study, the computational codes of the previous work were modified to incorporate the electrostatic dispersion equations and the algorithm shown in Fig. 2 into the PBM. Then, the bivariate PBM was verified using Whitby et al. (1965), Kasper (1981), Adachi et al. (1981), Oron and Seinfeld (1989a), Vemury et al. (1997), and Verdoold and Marijnissen (2009), who have typically been used for verifying electrostatic dispersion in PBMs (e.g., see Vemury et al., 1997; Xiangrong et al., 2006; Verdoold and Marijnissen, 2009).

4.1.1 Electrostatic dispersion of particles and ions

Results of the numerical analysis of Eqs. (4)–(6) were compared with those of the analytical solutions given by Whitby et al. (1965) and Kasper (1981), who assumed electrostatic dispersion of monodisperse aerosol and singly charged ions, respectively. Figure 3 shows time-dependent changes in particle and ion concentrations by electrostatic dispersion under three initial conditions: (i) monodisperse 1 µm particles with single positive charge, (ii) positive ions, and (iii) negative ions. Because the initial concentrations were similar, electrostatic dispersion rates of the particles and ions depended on their mobilities. Compared to the change in the particle concentration vs. time, the ion concentrations became more rapidly reduced by electrostatic dispersion because the ions were more mobile than the charged particles. These results obtained from the analysis of Eqs. (4)–(6) were in good agreement with the electrical dispersion rates computed by the analytical solutions.

Figure 3 Time-dependent changes in the concentrations of particles with j = +1 and positive and negative ions. The lines and symbols represent the results of analytical solutions (Whitby et al., 1965; Kasper, 1981) and numerical analysis of Eqs. (4)–(6) (this study), respectively.

4.1.2 Electrostatic dispersion of particles undergoing aggregation

Algorithm verification

Theoretical investigations have been extensively performed to predict electrostatic dispersion of particles undergoing aggregation (e.g., Adachi et al., 1981; Oron and Seinfeld, 1989a; Vemury et al., 1997; Verdoold and Marijnissen, 2009). In these investigations, electrostatic dispersion rates of particles are typically obtained by estimating the last term in Eq. (4). However, the sign of the electrostatic dispersion term depends on the space charge. To calculate electrostatic dispersion rates of particles as a function of the space charge of a system, the bivariate PBM used in this study employs the algorithm shown in Fig. 2. This algorithm was verified by comparing the simulation results of Eq. (4) with those of Adachi et al. (1981), Oron and Seinfeld (1989a), Vemury et al. (1997), and Verdoold and Marijnissen (2009), who predicted time-dependent changes in the concentrations of charged 1 µm particles by aggregation and electrostatic dispersion. For the comparison, the charging terms in Eq. (4) and ion balance (i.e., Eqs. 5 and 6) were neglected.

Figure 4 shows time evolution of the particle charge distributions under initially asymmetric uni- and bi-modal charge distributions. When Eq. (4) was solved without the algorithm, the simulation results were comparable to those of Adachi et al. (1981) and Oron and Seinfeld (1989a), respectively. However, discrepancies were found between the simulation results of the bivariate PBM executing the algorithm and those of Adachi et al. (1981) and Oron and Seinfeld (1989a). The discrepancies might arise from the treatment of the electrostatic dispersion term in Eq. (4) by the algorithm. Because the initial conditions of the test cases produced the negative space charge, electrostatic dispersion did not affect the concentrations of positively charged particles. Thus, the electrostatic dispersion term for the positively charged particles was neglected in the simulation of the bivariate PBM implementing the algorithm, while it was involved in the other cases. In addition, because of the negative space charge, the sign of the electrostatic term for the positively charged particles became positive. Therefore, the simulation results obtained from the bivariate PBM without the algorithm (e.g., Adachi et al., 1981) could slightly overestimate the concentration of positively charged particles that collide with negatively charged particles by electrostatic attraction. For other initially symmetric uni- and bi-modal particle charge distributions, the prediction results obtained from Eq. (4) including the algorithm were comparable to those of Vemury et al. (1997) and Verdoold and Marijnissen (2009) because the space charge was rarely formed during the simulations (Figs. S1 and S2 in the Supplement).

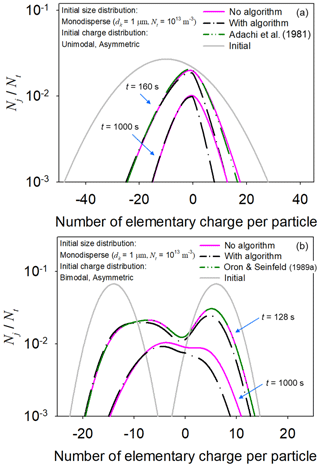
Figure 4 Time-dependent changes in the particle charge distributions predicted using the bivariate PBM and including and excluding the algorithm of Fig. 2, respectively. The simulation results obtained from solving Eq. (4) without the algorithm were in good agreement with those of Adachi et al. (1981) and Oron and Seinfeld (1989a) but were different from those obtained from solving Eq. (4) with the algorithm.

Comparison with measurements

The bivariate PBM including electrostatic dispersion was verified using the measurements of Adachi et al. (1981), who investigated the time evolution of the electrical mobility distribution of particles with an asymmetric bimodal charge distribution. Two peaks of the initial charge distribution were observed at j = −104 and 49. For comparison, simulations were performed with only the aggregation and electrostatic dispersion terms, separately.

Figure 5 shows the electrical mobility distribution of negatively charged particles at t = 5 min. The results of the simulation involving both aggregation and electrostatic dispersion were closer to the measurements than those including each process, separately. The discrepancies in the simulation results indicate that the bipolarly charged particles might simultaneously undergo aggregation and electrostatic dispersion because of their electrostatic interactions.

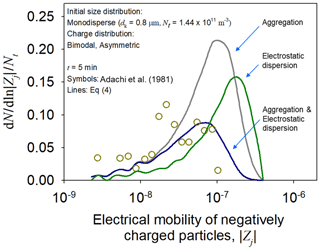
Figure 5 Electrical mobility distribution of negatively charged particles at t = 5 min. The symbols and lines represent the measurements of Adachi et al. (1981) and the simulation results of the bivariate PBM of this work, respectively.

It has been shown that the developed bivariate PBM can accurately calculate electrostatic dispersion rates of charged particles undergoing aggregation, as well as precisely computing the aggregation rates of particles accumulating charges (Kim et al., 2016). These verification tests suggest that the developed bivariate PBM can accurately predict charge and size distribution dynamics of particles undergoing charging, aggregation, and electrostatic dispersion.

4.2 Influence of radioactivity on time evolution of charge and size of radioactive particles

Charge and size distribution dynamics of radioactive particles was investigated with the bivariate PBM executing the developed algorithm. Similar to the previous tests, we assumed monodisperse particles with N_t = 10¹³ m⁻³. The initial charge distribution was estimated using Eq. (12). Simulation results for nonradioactive particles were provided as a reference.

4.2.1 Alpha decay vs. beta decay: effects of kinetic energy

Time-dependent changes in the charge and size distributions of ²³⁸Pu and ¹³¹I particles were investigated. ²³⁸Pu and ¹³¹I decay to ²³⁴U and ¹³¹Xe, respectively. Because ²³⁴U is a long-lived radionuclide with a half-life of 2.455×10⁵ years, and because ¹³¹Xe is a stable nuclide, these decay products are not expected to affect the activity of the radioactive particles during the period investigated. The properties of charged monodisperse ²³⁸PuO₂ particles (J_k = 2.84; d_k = 0.96 µm; A_Pu-238 = 1.92 Bq; Yeh et al., 1978) were used to postulate the initial charge distribution of ²³⁸Pu particles. For comparison, we assumed that the values of ¹³¹I particles for J_k, d_k, and A are comparable to those of the ²³⁸Pu particles.

Figure 6 shows changes in the charge and size distributions of the ²³⁸Pu and ¹³¹I particles vs. time. The initial charge distributions of the radioactive particles instantaneously shifted to the left and then became widely dispersed over time, while no such response was observed in the reference simulation (Fig. 6a). Radioactivity-induced charging and electrostatic dispersion of positive ions caused the horizontal movement of the particle charge distributions. The initial changes indicated that the ²³⁸Pu particles accumulated more negative charge than that acquired by the ¹³¹I particles. The different charging states affected the size growth of the radioactive particles due to aggregation (Fig. 6b).

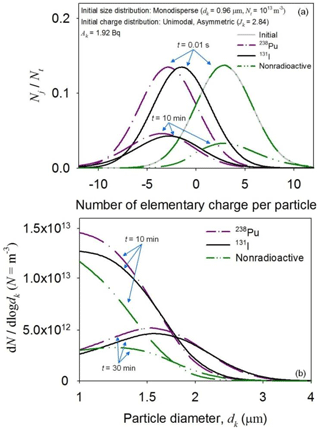
Figure 6 Time-dependent changes in the charge (a) and size (b) distributions of monodispersed ²³⁸Pu and ¹³¹I particles (d_k = 0.96 µm; N_t = 10¹³ m⁻³; A_Pu-238 = A_I-131 = 1.92 Bq). The simulation time is 30 min. The charge (a) and size (b) distributions of nonradioactive particles (A = 0) were given as a reference.

The different charge accumulation and aggregation rates of the radioactive particles were mainly attributed to their decay modes, which emitted alpha and beta particles of different energy levels. Because the kinetic energy of the alpha particles of ²³⁸Pu was much higher than that of the beta particles of ¹³¹I, the alpha-emitting particles produced more ion pairs than those generated by the beta-emitting particles. Due to the high mobility of negative ions, the production of more ion pairs led to the acquisition of many negative charges by more ²³⁸Pu than ¹³¹I particles (Fig. 6a). The positive charge accumulated via particle self-charging was immediately neutralized (the first term vs. the fourth and fifth terms in Eq. 4). Thus, the ²³⁸Pu particles aggregated less frequently due to stronger electrostatic repulsive forces generated between them (Fig. 6b).

Electrostatic dispersion indirectly influenced the particle charge and size distributions by affecting the time evolution of the ion concentrations. Although radioactivity-induced ionization produced ion pairs, the concentration of negative ions quickly increased at the early phase because many positive ions were rapidly removed by electrostatic dispersion caused by the initial positive space charge. The electrostatic dispersion of positive ions suppressed the increase in the positive ion concentration, which hindered the ion–ion recombination (see Eqs. 5 and 6). Due to the suppression of the ion–ion recombination, more negative ions were captured by the radioactive particles, thereby generating more negatively charged particles. The increase in the concentration of negatively charged particles modified the aggregation rates of the particles, since more particles were affected by strong electrostatic repulsive forces. The level of the indirect effect on the initial distribution movement of the ¹³¹I and ²³⁸Pu particles was unequal because the times needed to counterbalance the initial positive space charge were different (Fig. S3).

4.2.2 Beta decay of ¹³⁷Cs vs. beta decay of ¹³¹I

Time evolution of the charge and size distributions of ¹³⁷Cs and ¹³¹I particles was investigated. ¹³⁷Cs decays to ^137mBa, which is subsequently transformed into ¹³⁷Ba by gamma decay. In our assessment of the effects of the beta decay of these radionuclides on charge and size distributions, the influence of gamma decay was not considered. Because fission products can be carried by sulfate aerosols (Baltensperger et al., 1987), it was assumed that (i) the beta-emitting radionuclides are embedded in (NH₄)₂SO₄ aerosols and that (ii) the radioactive fractions of the ¹³⁷Cs particles and ¹³¹I particles are similar. The initial charge distribution of ¹³⁷Cs-(NH₄)₂SO₄ particles was obtained from the properties of charged monodisperse particles containing radioactive cesium (J_k = 0.75; d_k = 0.82 µm; A_Cs-137 = 12.8 mBq; Gensdarmes et al., 2001). Using the radioactivity level of radioactive cesium, the fractions of ¹³⁷Cs and (NH₄)₂SO₄ per particles can be obtained (Clement et al., 1995). For comparison, it was assumed that the fractions of ¹³¹I and (NH₄)₂SO₄ per particle are similar to those of the ¹³⁷Cs particles.

Figure 7 shows time-dependent changes in the charge and size distributions of the ¹³⁷Cs and ¹³¹I particles. Similar to the initial distribution movements shown in Fig. 6, the initial charge distributions of the radioactive particles were rapidly shifted to the left in contrast to the reference simulation (Fig. 7a). However, the charge distribution of the ¹³⁷Cs particles became symmetric, while that of the ¹³¹I particles remained asymmetric, which affected the time evolution of the particle size distributions (Fig. 7b).

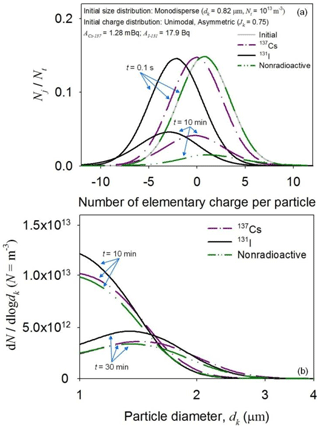
Figure 7 Time-dependent changes in the charge (a) and size (b) distributions of monodispersed ¹³⁷Cs and ¹³¹I particles (d_k = 0.82 µm; N_t = 10¹³ m⁻³; A_Cs-137 = 1.28 mBq; A_I-131 = 17.9 Bq). The simulation time is 30 min. The charge (a) and size (b) distributions of nonradioactive particles (A = 0) are shown for comparison.

The dissimilar charging and aggregation rates of the radioactive particles were largely attributed to the different levels of radioactivity. Despite the similar radioactive fraction per particle, A_I-131 ≈ 17.9 Bq, while A_Cs-137 ≈ 12.8 mBq because the radioactivity level of short-lived radionuclides is higher than that of long-lived radionuclides when their radioactive fractions are similar ($t_{\mathrm{1}/\mathrm{2},\mathrm{I}\text{-}\mathrm{131}}$ ≈ 8 d, while $t_{\mathrm{1}/\mathrm{2},\mathrm{Cs}\text{-}\mathrm{137}}$ ≈ 30.1 years) (Clement et al., 1995; Hu et al., 2014). Due to the different radioactivity levels, the ¹³⁷Cs particles produced much fewer ion pairs compared to those produced by ¹³¹I particles. Thus, the indirect effects of electrostatic dispersion mainly forced the initial distribution changes in the ¹³⁷Cs particles, while both charging and electrostatic dispersion affected the dispersion of the ¹³¹I particles (Fig. 7a). Negative charge on the ¹³¹I particles produced strong electrostatic repulsive forces, thereby hindering their size growth by aggregation (Fig. 7b).

Although the mean charge of the ¹³⁷Cs and nonradioactive particles was similar at the very early phase (t = 0.1 s), their charge and size evolved differently with time (Fig. 7a and b). The discrepancies in the distributions largely arose from the effects of electrostatic dispersion. In contrast to the ¹³⁷Cs particles, the positive space charge of the system containing nonradioactive particles continuously decreased due to electrostatic dispersion of the particles. Thus, the concentration of the nonradioactive particles decreased more rapidly with time.

It has been shown that radioactive decay can induce dispersion of the charge and size distributions of radioactive particles. The distributions evolved differently as a function of decay modes, radioactivity levels, and initial charge. These results suggest that time evolution of the charge and size distributions of radioactive particles can significantly differ from that of nonradioactive particles in the atmosphere.

4.3 Potential effects of radioactivity on background aerosols

The Fukushima nuclear plant accident resulted in atmospheric dispersion of many radionuclides, such as ¹³⁷Cs, thereby increasing air dose rates in many areas of Japan. Changes in the concentrations of charged background aerosols were investigated as a function of air dose rates observed in Iwaki, which is tens of kilometers away from the accident site (Katata et al., 2012). The observed values were converted into ionization rates by assuming that ionizing radiation produces 2.2×10¹¹ ion pairs ${\mathrm{m}}^{-\mathrm{3}}\mathrm{\mu }{\mathrm{Gy}}^{-\mathrm{1}}$ (Subramanian et al., 2012). We assumed log-normal distributions of uncharged background aerosols to obtain the initial particle charge and size distributions (Kim et al., 2016).

Figure 8 illustrates changes in the concentrations of charged and uncharged background aerosols vs. air dose rates. The total particle concentration gradually decreased with time due to particle aggregation. At an early stage, background ionization led to diffusion charging, which created a discrepancy in the concentrations of charged particles because of their dissimilar properties. However, as ionizing radiation occurred, the concentration of negatively charged particles became much higher than that of positively charged particles due to changes in ion concentrations. Similar results were obtained for simulations using different ion properties given by Kim et al. (2016) and air dose rates measured at other places (Katata et al., 2012). These results suggest that if radiation fields are created in the atmosphere, then negatively charged particles may be more easily detected during field measurements of charged particles.

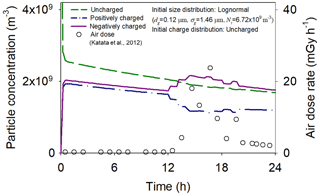
Figure 8 Changes in the concentrations of charged and uncharged particles vs. air dose rates. Lines represent the simulation results. Symbols represent air dose rates measured at Iwaki, Japan, after the Fukushima nuclear plant accident (Katata et al., 2012).

The generation of more negatively than positively charged particles indicates that the background aerosols may interact more frequently with beta-emitting radionuclides in gas and particulate phases, which could acquire positive charge by beta emission. Recent experiments performed at the microscopic level showed that electrostatic interactions can enhance uptake of water molecules by charged particles (Kweon et al., 2015), suggesting that more radioactive gas molecules might be accumulated on the background aerosols with negative charge. Also, using the average radioactivity of single ¹³⁷Cs particles contained in the first plume of the Fukushima accident (Adachi et al., 2013) and the maximum air dose rates observed in Iwaki, calculations suggest that particles containing ¹³⁷Cs might be positively charged because of their self-charging during long- and short-range transport (not shown). Thus, the negatively charged background aerosols might more easily aggregate with the positively charged radioactive particles due to electrostatic attractive forces among them. These results suggest that radioactivity, which creates many ion pairs, may facilitate acquisition of radioactivity by background aerosols and affect their charging behavior and size growth.

4.4 Monovariate and monodisperse PBMs

4.4.1 Verification

The bivariate PBM can be replaced by the monovariate and monodisperse PBMs in model studies of transport of contaminants carried by charged particles, as well as investigations using particle measurement systems. The simpler PBMs were verified using the bivariate PBM; we focused on testing the third term of Eq. (13) and the incorporation of the charging terms of Eq. (4) into Eq. (15), respectively. It is assumed that (i) particles are nonradioactive and uncharged, (ii) the initial particle size distribution is monodispersed, and (iii) n_± = 10³N₀ during simulation. For reference, simulation results were obtained using Eq. (4) in the absence of the electrostatic dispersion term.

Simulation results of the bivariate PBMs are depicted in Fig. 9. Particles were charged by capturing ions. Because the ion concentrations were constant in the simulation, the particle charge caused electrostatic dispersion of the charged particles, leading to discrepancies in the results of the bivariate PBM and the reference simulation (bivariate PBM vs. reference). Compared with the monodisperse PBM, the simulation results of the monovariate PBM were in better agreement with those of the bivariate PBM (bivariate PBM vs. monovariate PBM; bivariate PBM vs. monodisperse PBM). Compared to the bivariate PBM, the particle size predicted by the monodisperse PBM was larger. After 1 h, the mean sizes predicted by the monodisperse and bivariate PBMs were 1.04 and 0.89 µm, respectively, indicating a difference of 16.9 %. This difference increased with time (e.g., 29.7 % after 3 h).

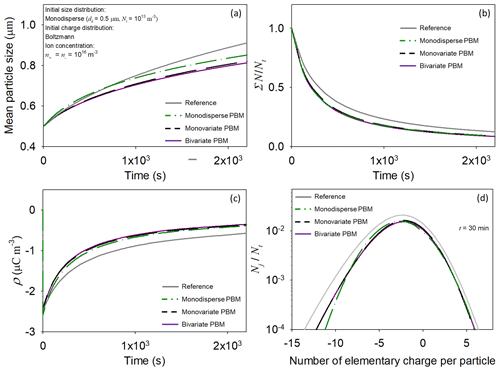
Figure 9 Time-dependent changes in the mean size (a) and total concentration (b) of particles, the space charge density (c), and particle charge distribution (d) in a spatially homogeneous atmospheric system. Reference refers to simulation results obtained using Eq. (4) in the absence of the electrostatic dispersion term.

The monovariate PBM accurately predicted both particle size and charge distributions, while the monodisperse PBM forecasted only the particle charge distribution.

4.4.2 Application of monovariate PBM

In case of a severe nuclear reactor accident, highly radioactive particles in a pressurized water reactor containment system may be released into the atmosphere. The monovariate PBM, which can predict both particle charge and size distributions, was applied to investigate the charging of highly radioactive particles and subsequent effects on particle collision after the release. The initial conditions were quoted from the containment system postulated by Clement et al. (1995), where radioactivity induced the charging of ¹³¹I particles (d_g = 0.4 µm; σ_g = 2; N_t = 10⁹ m⁻³).

Figure 10 shows changes in the mean charge and average collision efficiency of the ¹³¹I particles after the release into the atmosphere. The charging state of the ¹³¹I particles was immediately modified in the atmosphere because the radioactive particles acquired many positive charges, while diffusion charging counterbalanced self-charging (Fig. 10a). The modification of the charging states affected the particle collision efficiency because strong electrostatic attractive and repulsive forces were generated between the ¹³¹I particles (Fig. 10b), indicating that the charging and aggregation patterns of highly radioactive particles in the atmosphere can be different from those in the containment system. The effects of electrostatic dispersion were insignificant due to the low space charge of the containment system and high radioactivity levels of the particles.

Figure 10 Time evolution of mean charge (a) and average collision efficiency (b) of ¹³¹I particles released from postulated pressurized water reactor containment.

5 Conclusions

Charge and size evolutions of atmospheric particles involving radioactive particles are vital to transport modeling of radioactivity, as well as in situ particle measurements in the atmosphere. This study presents the bivariate PBM, taking into account radioactivity-induced charging, aggregation, and electrostatic dispersion, as well as ion balance. Using the PBM, it has been shown that size and charge distribution dynamics of radioactive particles can be substantially different from those of nonradioactive particles because of radioactivity-induced charging and electrostatic dispersion, which subsequently can affect particle growth due to aggregation. These results suggest that the bivariate PBM can be used to include radioactivity-induced charging and electrostatic dispersion, and the subsequent effects on particle aggregation in predictive studies of radioactivity transport. Furthermore, ionizing radiation may affect the acquisition of charge and radioactivity by background aerosols, possibly influencing the in situ detection of charged particles in radiation fields. The bivariate PBM has been simplified to two different PBMs, which can be applied to model studies of radioactivity transport. This study offers useful insight into the dynamic behavior of particles in atmospheric systems with radiation sources.

Appendix A: Nomenclature

Ak	Radioactivity of single particles
B	Particle mobility
Dk	Particle diffusion coefficient
dk	Particle diameter
e	Electrical charge
F	Aggregation frequency
Jk	Mean charge of size k particles
j	Number of elementary charge carried by individual particles
kB	Boltzmann coefficient
l, m	Size bin numbers
M	Total number of size bins
m±	Mass of positive and negative ions

Nk,j	Number concentration of size k particles carrying elementary charge j
Nt	Total number concentration of particles
n±	Concentrations of positive and negative ions
q	Production rate of ion pairs
qe	Production rate of electrons
s	Self-charging coefficient
T	Temperature
t	Time
V	Average volume of particles
Vt	Total volume of particles
χk	Particle mass
αBr	Collision efficiency for Brownian motion
αrc	Recombination rate coefficient of positive and negative ions
${\mathit{\beta }}_{k,j}^{\pm }$	Ion particle attachment coefficients
βBr	Collision frequency for Brownian motion
δKr	Kronecker delta
ε	Permittivity of vacuum
η	Property distribution factor between two size bins
μ±	Mobilities of positive and negative ions
ρ	Space charge density
σk	Standard deviation